Flow around three cylinder in equilaterial triangular arrangements

Table of Contents

1. Presentation of the test case
2. Configuration files
- 2.1. cfg file
- 2.2. json file
3. Results
- 3.1. Running the case:
Bibliography

this benchmark is based on [chen-2020].

1. Presentation of the test case

1.1. Presentation

This study is based on the flow of a fluid in front of 3 circular and identical cylinders. The cylinders are arranged in an equilateral rectangle, one of the cylinders is placed upstream and the other two side by side downstream.

In this test case, we are particularly interested in the effect of the spacing ratio L/D and the number of Reynolds Re on the flow, where L is the center-to-center spacing of the cylinder and D is the cylinder diameter.

The numerical results obtained in this study, will be compared with those found in the literature, for different gaps \(L/D \in [1,6\)] and a Reynolds number \(Re \in [50,300\)].

1.2. Geometry setting

The arrangement of the cylinders in the calculation area \(\Omega\) is shown in the figure below :

Figure 1. The geometric setting for the 3 cylinder with equilaterial triangle arrangement

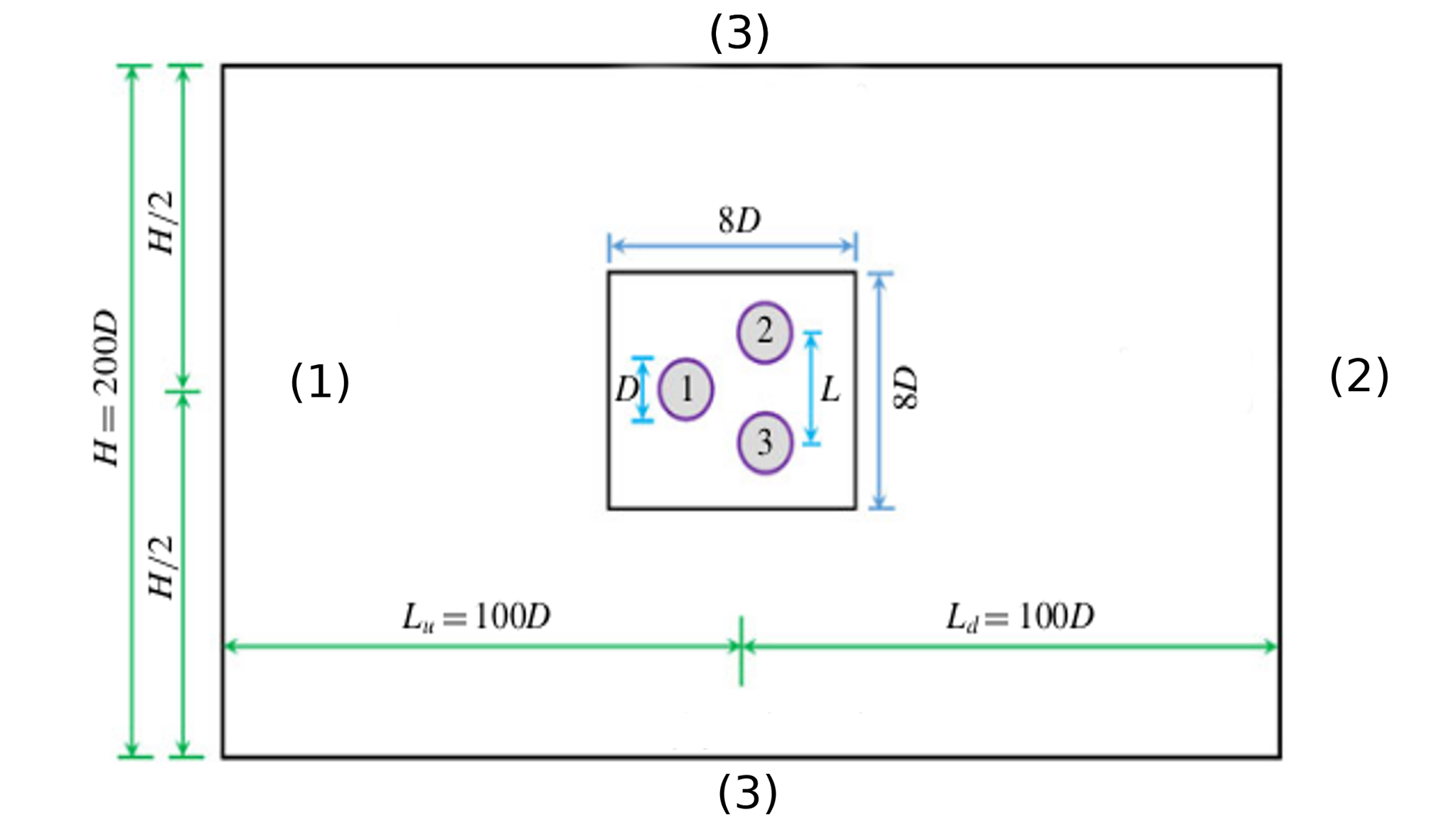
We provide here the basic geometry used in Gmsh to describe \(\Omega\).

Geo file

//GMSH
D=1.5;
L_sur_D=1.1;
L=D*L_sur_D;
H=200*D;
h=8;
Ld=100*D;
Lu=-100*D;
//caree
Point(1) = {0, 0, 0,h};
Point(2) = {Ld,H/2,0,h};
Point(3) = {Ld,-H/2,0,h};
Point(4) = {Lu,H/2,0,h};
Point(9) = {Lu,-H/2,0,h};
//+
Line(1) = {2, 3};
//+
Line(2) = {3, 9};
//+
Line(3) = {9, 4};
//+
Line(4) = {4, 2};
//+
Point(23) = {-L, 0, 0, h};//centre 1
//+
Point(17) = {L, L_sur_D, 0, h};//centre 2
//+
Point(18) = {L, -L_sur_D, 0, h}; //centre 3
//+
Point(24) = {L+D/2, L_sur_D, 0, h};
//+
Point(25) = {L-D/2, L_sur_D, 0, h};
//+
Point(26) = {L-D/2, -L_sur_D, 0, h};
//+
Point(27) = {L+D/2, -L_sur_D, 0, h};
//+
Point(28) = {-L-D/2, 0, 0, h};
//+
Point(29) = {-L+D/2, 0, 0, h};
//+
Circle(9) = {24, 17, 25};
//+
Circle(10) = {25, 17, 24};
//+
Circle(11) = {26, 18, 27};
//+
Circle(12) = {27, 18, 26};
//+
Circle(14) = {29, 23, 28};
//+
Circle(15) = {28, 23, 29};
//+
//surface
//+
Line Loop(1) = {9, 10};
//+
Line Loop(2) = {12, 11};
//+
Line Loop(3) = {14, 15};
//+
Line Loop(4) = {1, 2, 3, 4};
//+
Plane Surface(1) = {1, 2, 3, 4};
//+
Physical Line("inlet") = {3};
//+
Physical Line("outlet") = {1};
//+
Physical Line("wall1") = {4};
//+
Physical Line("wall2") = {2};
//+
Physical Surface("omega") = {1};

The Data provided on the whole \(\Omega\) domain allows us to have conditions at the specified limits, the table below summarize these data.

Table 1. Geometric data table
Notation	Description	Value	Unit
\(D\)	cylinder diameter	-	\(m\)
\(L\)	the center-to-center spacing of the cylinder	-	\(m\)
\(H\)	side of the domain	200D	\(m\)
\(U\)	Inlet velocity	\(\frac{Re}{D}\)	\(m/s\)

1.3. Physical setting

The Physical parameters are:

Table 2. Physical data table
Notation	Description	Value	Unit
\(\rho\)	Density	1	\(Kg/m^3\)
\(\mu\)	Dynamic viscosity	1	\(Pa.s\)

1.4. Boundary conditions

In this study 3 boundary conditions are imposed: Inlet condition, Outlet condition and the Wall condition.

Inlet condition

On boundary (1) a Dirichlet-type condition is imposed and a Poiseuille profile is placed as an entry condition, it’s defined by:

\[u = U \\ v = 0\]

json configuration for the inlet boundary condition

"inlet":
{
   "expr":"{Re/D,0}:Re:D"
}

Wall conditions

On the limits (3), i.e. on the upper and lower wall we have :

\[\frac{\partial{u}}{\partial{x}}=0\\ \frac{\partial{v}}{\partial{x}}=0\]

json configuration for the wall boundary condition

"wall1":
{
    "expr":"0"
},
"wall2":
{
    "expr":"0"
}

Outlet condition

On boundary (2) (i.e the exit boundary condition) a Neumann-type condition is imposed

\[\frac{\partial{u}}{\partial{y}}=0\\ v=0\]

json configuration for the outlet boundary condition

"Neumann_scalar":
 {
     "outlet":
      {
          "expr":"0"
      }
 }

1.5. Mesh

We move on to meshing to generate fully structured uniform triangular cells, the figure below shows a part of the generated mesh:

Figure 2. generated mesh for case \(L/D = 1.1\)

Figure 3. represents a zoom-in view of the previous mesh

2. Configuration files

2.1. cfg file

directory=resulats/cylinders/P1

[case]
discretization= P2P1G1
dimension=2

[fluid]
filename=$cfgdir/cylinders.json
mesh.filename=$cfgdir/cylinders.geo
gmsh.hsize=8

solver= Newton #Oseen #Newton #Picard,Newton
linearsystem-cst-update=false
jacobian-linear-update=false

snes-monitor=true
pc-type= gams #gasm,lu
snes-rtol=1e-10

2.2. json file

Here the full json configuration file

Json file

{
    "Name": "three circular cylinders in equilateral-triangular arrangements",
    "ShortName":"flow past",
    "Models":
    {
         "equations": "Navier-Stokes"
    },
    "Materials":
    {
        "omega":
        {
            "rho":"1",
            "mu":"1"
        }
    },
    "Parametres":
    {
      "Re":"100",
      "D":"1.5"
    },
    "BoundaryConditions":
    {
        "velocity":
        {
            "Dirichlet":
            {
                // tag::inlet[]
                "inlet":
                {
                   "expr":"{Re/D,0}:Re:D"
                }
                // end::inlet[]

             },
            "outlet":
            {
             // tag::walls[]
                 "wall1":
                 {
                     "expr":"0"
                 },
                 "wall2":
                 {
                     "expr":"0"
                 }
             // end::walls[]
            }
        },
        "fluid":
        {
          // tag::outlet[]
          "Neumann_scalar":
           {
               "outlet":
                {
                    "expr":"0"
                }
           }
          // end::outlet[]
        }
    },
    "PostProcess":
    {
        "Exports":
        {
            "fields":["velocity"]
        }
    }
}

3. Results

3.1. `Running the case`:

The command line to run this cases is

mpirun -np 4 feelpp_toolbox_fluid--config-file cylindre.cfg--fluid.snes-monitor=1--fluid.gmsh.hsize=8

Once the command is executed the results are exported to ParaView for viewing the flow by executing:

rsync -avz atlas.math.unistra.fr:/feel

Bibliography

[chen-2020] Numerical simulations of flow past three circular cylinders in equilateral-triangular arrangements Chen, Weilin, Ji, Chunning, Alam, Md. Mahbub, Williams, John, Xu, Dong, Journal of Fluid Mechanics2020 / 05 Vol. 891, Download PDF