Fluid-structure interaction in a tube
a
1. Introduction
Blood flow and blood vessel walls mechanically deform each other. We study this fluid-structure interaction in a simplified geometry : a tube. The tube is a simplified model for a part of either an artery or a vein. The inside of the tube represents blood, and its wall has a certain thickness to represent the vessel wall.
More specifically, we use this simple test to study the variability of the external constraints. This corresponds to the reaction of the surrounding tissues to the deformation of the blood vessel wall. These tissues may be softer or stiffer in certain parts of the body.
2. Geometry
The tube geometry is adapted from the Feel++ wavepressure3D FSI example. // TODO link It consists in a cylinder (the fluid domain) with an external layer (the solid domain). The surface between the two domains is the fluid-structure interface.

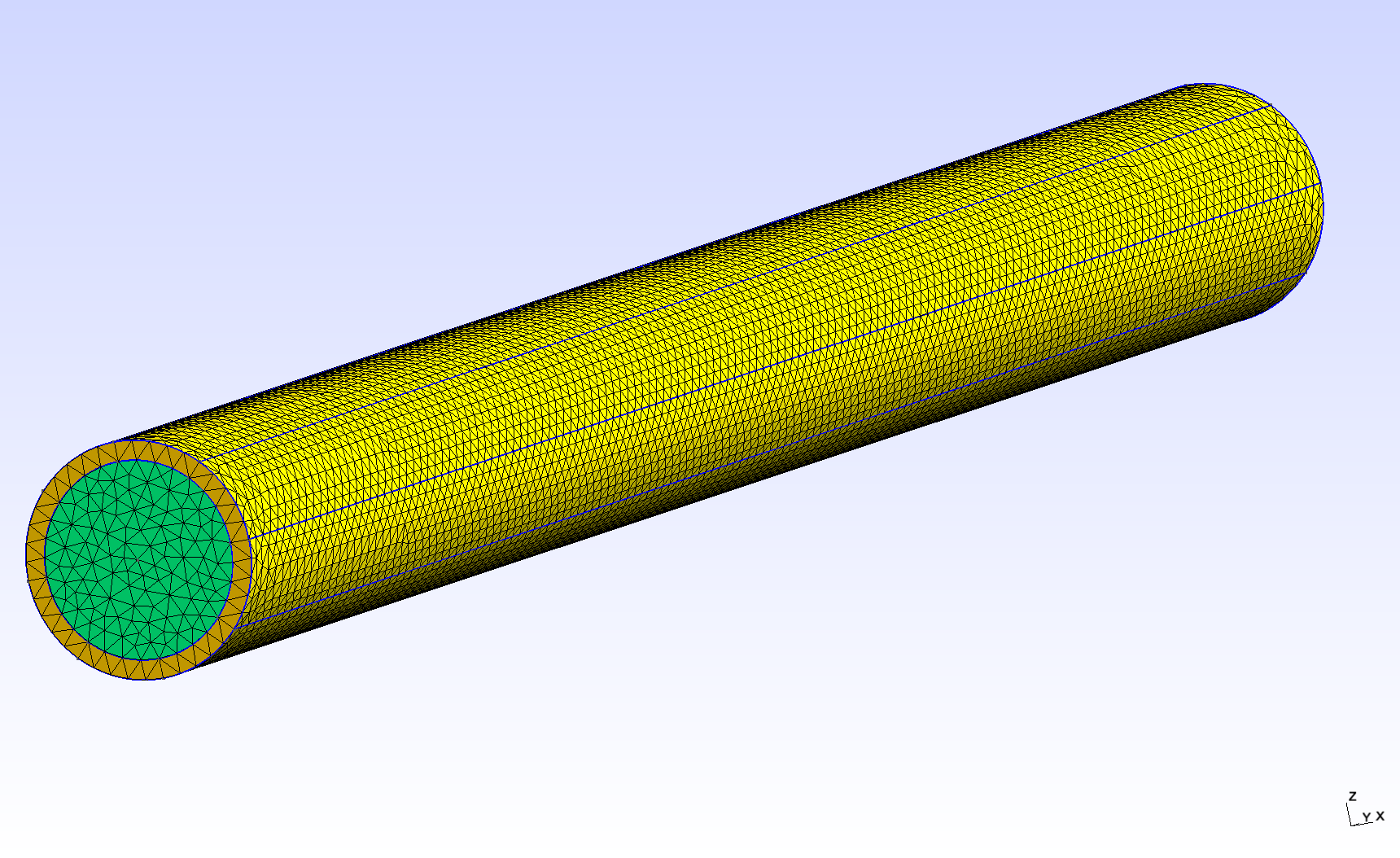
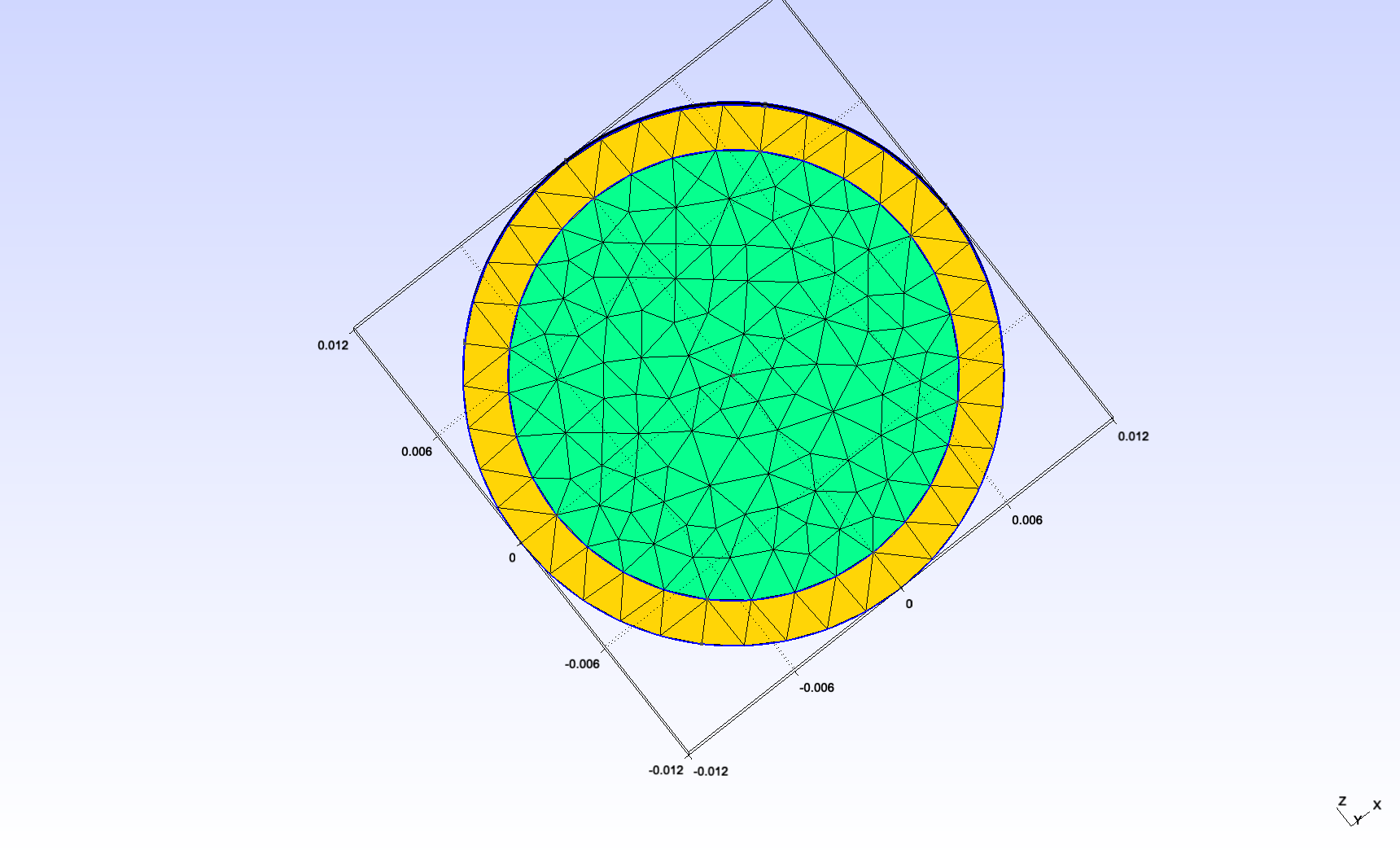
2.1. Dimensions
We changed the scale and the length/diam ratio as follows :
internal radius |
\(0.01mm\) |
external radius |
\(0.012mm\) |
length |
\(0.3mm\) |
This makes the tube reasonably close to the dorsal aorta (radius \(~0.01mm\)).

2.2. Physical measures and units
We use the following physical input expressed in \(mm, g, s\)
/ / I will include this a csv later
For the fluid:
Notation |
Quantity |
Value |
Units (mm, g, s) |
\(\boldsymbol{u}_f\) |
fluid velocity |
\( 1\times 10^{-1} \) |
\( mm \cdot s^{-1} \) |
\(\rho_f\) |
fluid density |
\( 1 \times 10^{-3} \) |
\( g \cdot mm^{-3}\) |
\(\mu_f\) |
dynamic viscosity |
\( 2.2 \times 10^{-3} \) |
\( g \cdot mm^{-1} \cdot s^{-1}\) |
And for the solid:
Notation |
Quantity |
Value |
Units (mm, g, s) |
\(E_s\) |
Young modulus |
\( 3 \times 10^3 \) |
\( g.mm^{-1}.s^{-2} \) |
\(\nu_s\) |
Poisson’s ratio |
\( 0.3 \) |
dimensionless |
\(\rho_s\) |
solid density |
\( 1.2 \times 10^{-3} \) |
\( g.mm^{-3} \) |
3. Symmetric external constraints
We start with a simple case. Here, the constraint is not variable, it is the same all around the blood vessel.
3.2. Boundary conditions
We use the following boundary conditions for the fluid:
-
Dirichlet condition at the inlet : constant parabolic velocity profile (Umax = U0)
-
Neumann condition at the outlet : free outlet
And for the solid:
-
Dirichlet condition at the "inlet ring" : the displacement is 0
-
Neumann (scalar) condition at the "outlet ring" : the structure is free to move
-
Robin condition at the exterior surface to model the surrounding tissue constraint : for z>0, and for z<0, the coefficient is the same : 100.
3.3. Solvers settings
3.3.1. Dirichlet-Neumann FSI coupling scheme
We start with a Dirichlet-Neumann semi-implicit scheme, using the following settings:
Name |
Value |
tolerance |
\( 1 \times 10^{-5} \) (default) |
maximum fixed-point iterations |
\( 1000 \) (default) |
Robin-Robin FSI coupling scheme
We also try a Robin-Robin semi-implicit scheme with the following input:
Name |
Value |
\( \gamma \) |
\( 2500 \) (default) |
\( \gamma_0 \) |
\( 1 \) (default) |
\( \alpha \) |
\( 1 \) (default) |
maximum fixed-point iterations |
\( 3 \) |
For now, this does not work. The displacement relative residual does not converge to 0 fast enough. (A video of the problem could be added here)
We should work on this problem: - It could be a coupling parameters tuning issue ? - We could try using a Windkessel model for the fluid outlet.