Zero Mean Slopes

1. Motivation

The surface of the object we study might be slightly globaly inclined. If we can still reconstruct the surface, regarding the size of the local slopes, interesting details are harder to read.

Figure 1. Reconstruction of the Etalon inclined (3D)

Figure 2. Reconstruction of the Etalon inclined (2D)

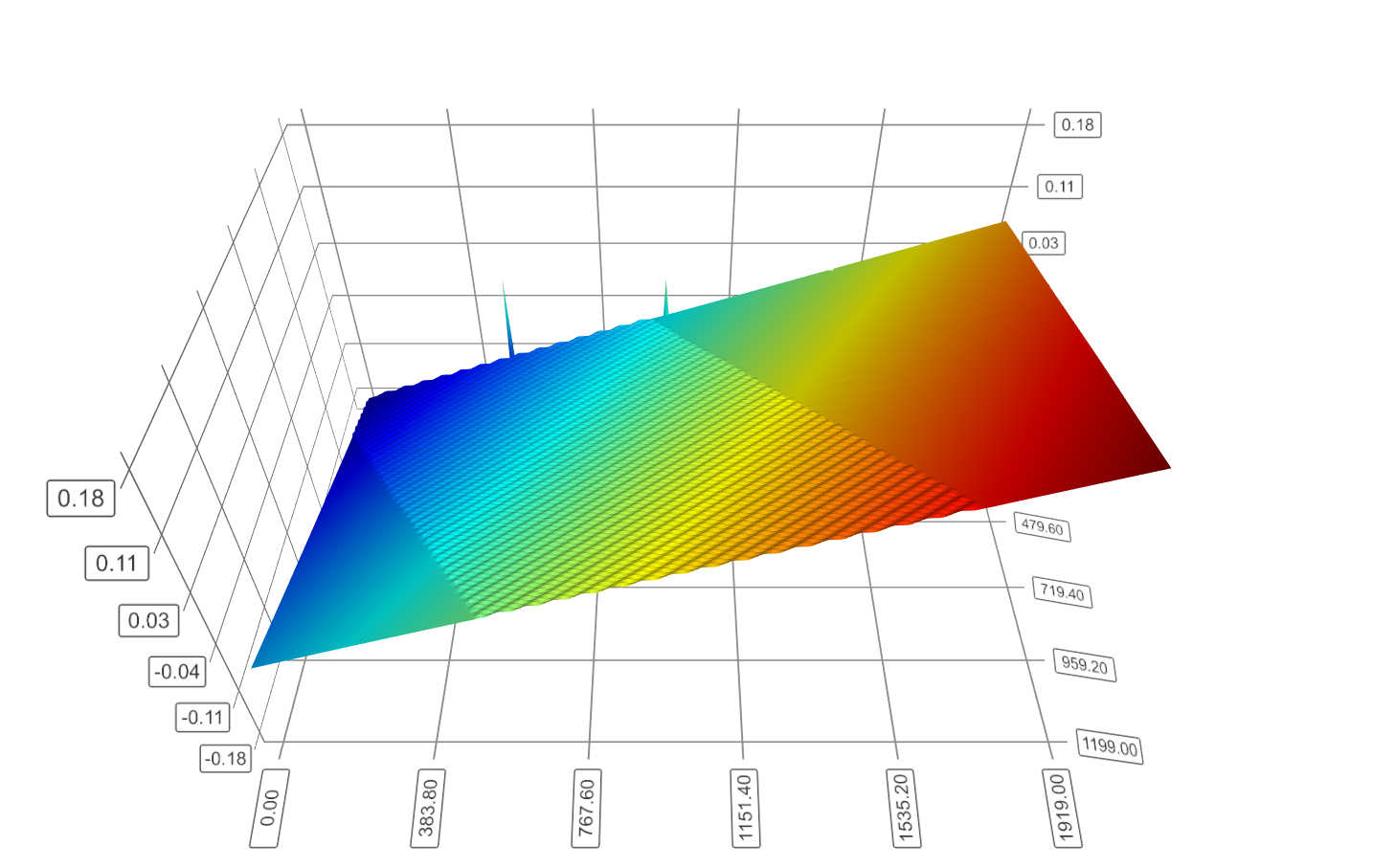
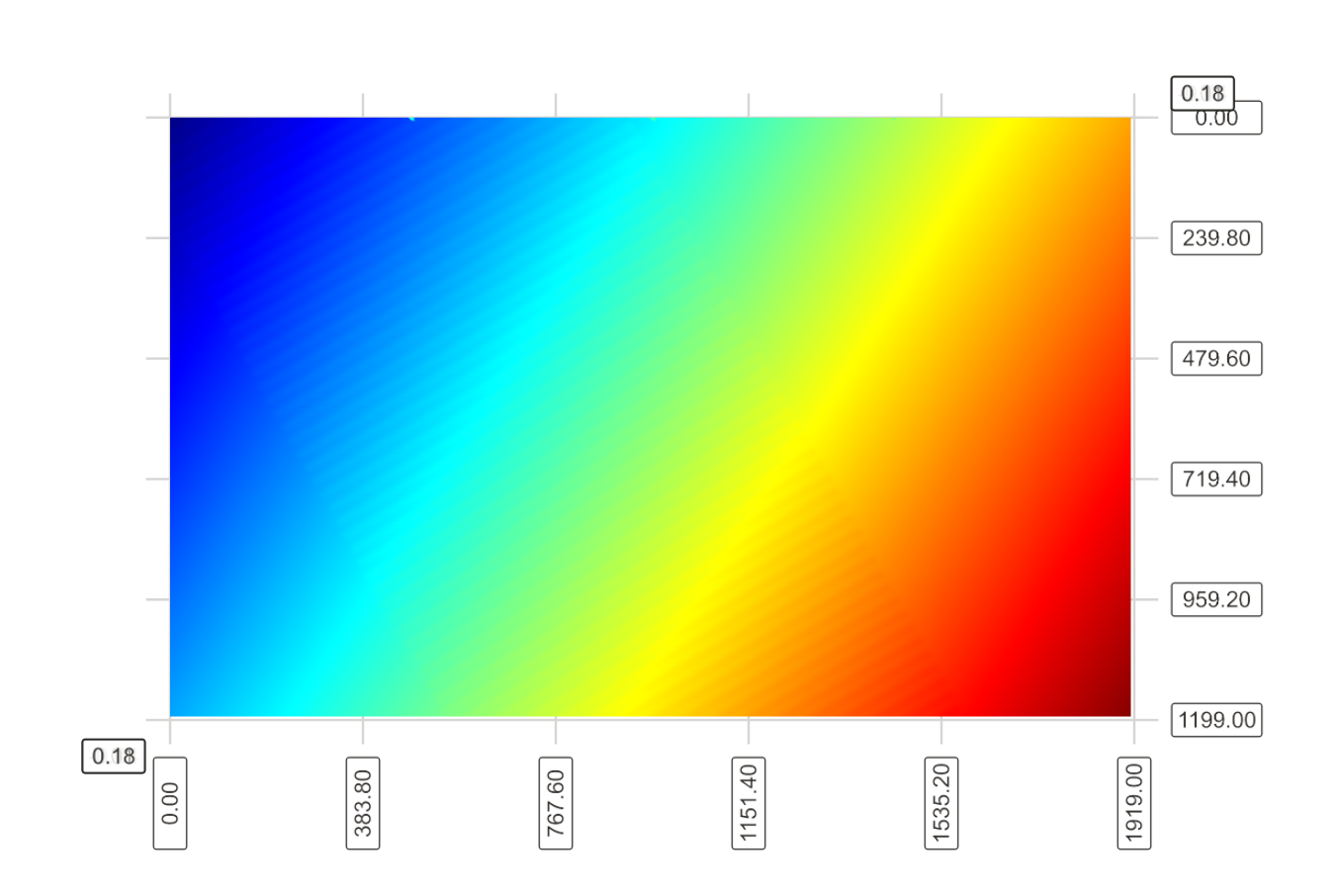
If in 3D we can still see the waves, in the 2D representation they are almost invisibles.

2. Strategy

To fix that problem, we can either :

Find out what is the global slope of the surface (by knowing the exact 3D-location of 3 extreme points of the surface and computing the plane linking them to remove its slope to our slopes files)

This would be the best solution to ensure the reconstruction works in any case scenario however finding out the exact 3D-location of any point is a really difficult information to get. We must choose another way.

Remove the mean of slopes to our slopes maps

Let suppose that the surface is globaly flat i.e. \(p(x, y) = \alpha + g(x, y)\) and \(q(x, y) = \beta + h(x, y)\) with g and h zero mean functions, then we just need to study \(g(x, y)\) and \(h(x, y)\) instead of \(p(x, y)\) and \(q(x, y)\).

If this is not the case, doing so will cause a loss of information and will lead to the creation of artefacts.

In practice, the method used in Polymap to compute slopes from phases data needs the object to be globaly flat to be studied with Polymap.

Finding the optimal plane that is the closest to the curve might be a working solution that doesn’t make any requirement on the object. (See the singular value decomposition algorythm)

3. Implementation

if ( boption( "polymap.pmean" ) )
{
    auto mpx = mean( _range = elements( support( Vh ) ),
                        _expr = idv( px ) )( 0, 0 ); (1)
    auto mpy = mean( _range = elements( support( Vh ) ),
                        _expr = idv( py ) )( 0, 0 );
    px.add( -mpx ); (2)
    py.add( -mpy );
    mpx = mean( _range = elements( support( Vh ) ),
                _expr = idv( px ) )( 0, 0 ); (3)
    mpy = mean( _range = elements( support( Vh ) ),
                _expr = idv( py ) )( 0, 0 );
}

1	Computing mean horizontal/vertical slope values on feelpp objects
2	Removing those values from the matrixes used to define slopes making them 0-mean
3	Setting the feelpp objects to 0-mean

The boolean parameter polymap.pmean is by default set to true

4. Results

Figure 3. Reconstruction of the Etalon un-inclined (3D)

Figure 4. Reconstruction of the Etalon un-inclined (2D)

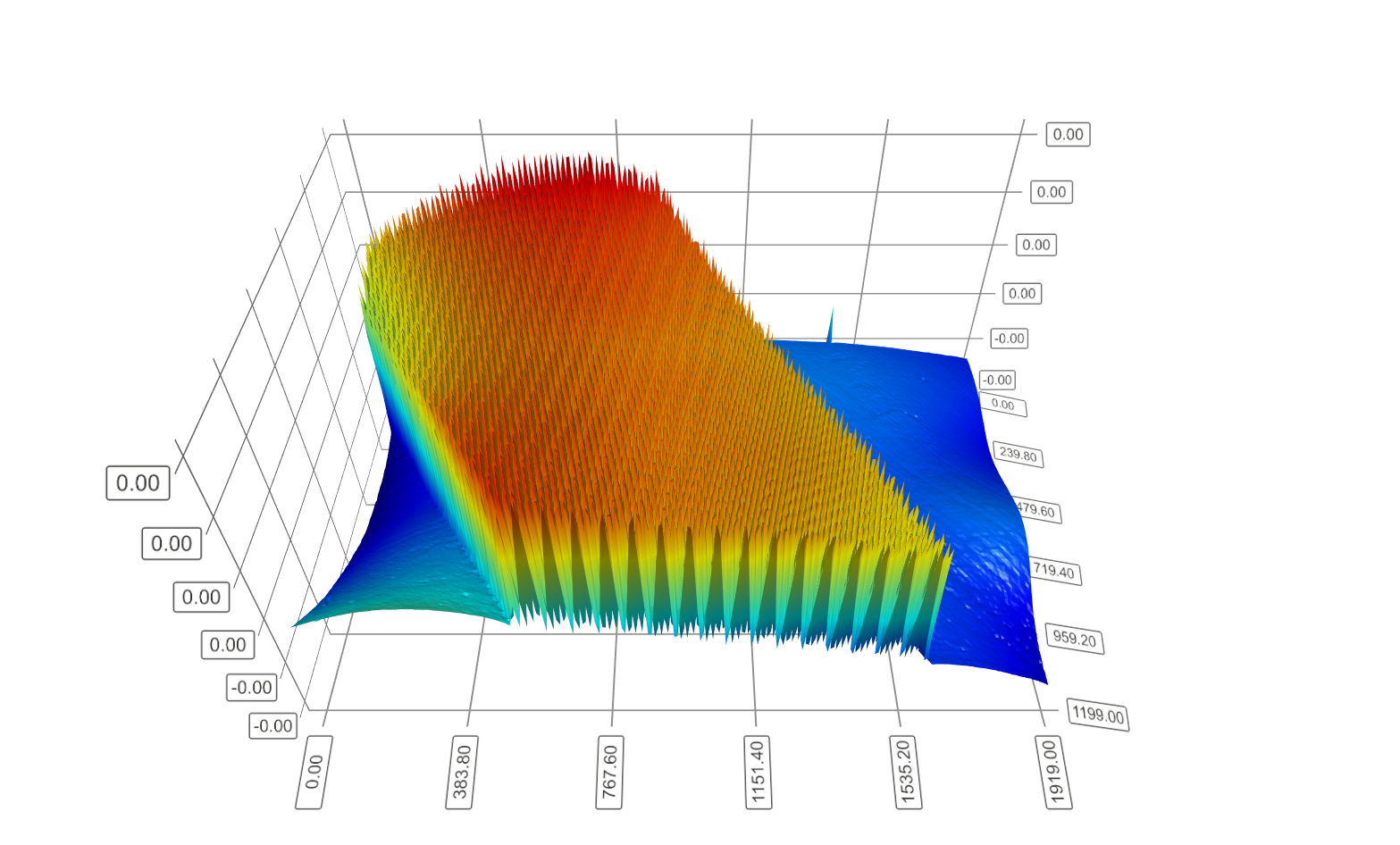
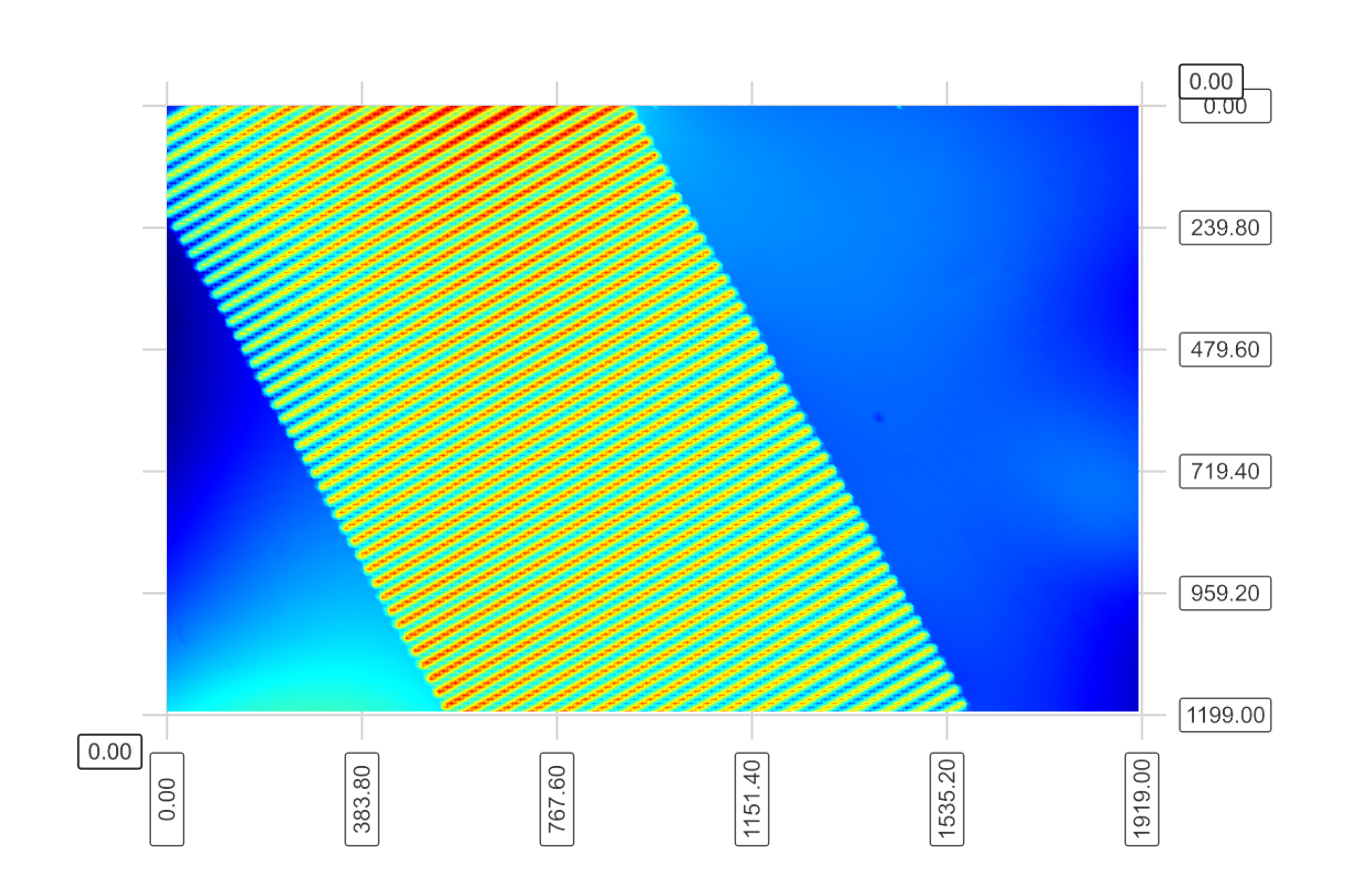
The local curves are now far more readable than above. However we don’t know for sure if the surface reconstructed outside of the object (the blue part on Fig. 4 ~ Reconstruction of the Etalon un-inclined) is really as curved as it appears of it is an artifact as discussed earlier.