Polygonal selection
When studying certain objects, we know in advance that in certain areas, the reflection will be outside of the camera because of the geometry of the object.
Furthemore, we often need to study the edge of an object and to do so, the edge of the object need to be placed in the center of the picture, making a huge part of the picture empty.
In either case, reconstructing only a part of the picture is faster (since it will reduce the number of unknowns of the system we have to solve in order to reconstruct the surface) and more readable (because there will be no misleading data).
Holo3 will provides futures mask.hbf files and this piece of code might never be used again but during the phase of developpment of the application it was helpfull to create a custom mask generator to test the reconstruction without waiting for HOLO3 to make a new mask each time.
|
1. Implementation
mask_t computeMask(int nrows, int ncols, std::vector<point_t> const pointList)
{
Eigen::MatrixXi x = Eigen::RowVectorXi::LinSpaced(ncols, 0, ncols)
.colwise().replicate(nrows);(1)
Eigen::MatrixXi y = Eigen::VectorXi::LinSpaced(nrows, 0, nrows)
.rowwise().replicate(ncols);
mask_t isInside = mask_t::Ones(nrows, ncols);
for (auto it = pointList.begin(); it != pointList.end(); ++it)
{
point_t ptA = *it;(2)
point_t ptB = (std::next(it)!=pointList.end()) ? *std::next(it) : *pointList.begin() ;
auto xA = ptA.first;
auto yA = ptA.second;
auto xB = ptB.first;
auto yB = ptB.second;
auto a = yA-yB;
auto b = xB-xA;
auto c = a*xA + b*yA; (3)
isInside = ( isInside && ((x.array()*a + y.array()*b) <= c) );(4)
}
[...]| 1 | Creating two matrices of coordinates : the pixel i,j has coordinates (x(i,j) y(i,j)) |
| 2 | Reading each point of pointList and its follower. If the point is the last point, close the loop by saying the follower is the first point |
| 3 | Setting the equation of the oriented line made by those two points |
| 4 | A point "is inside" the polygon if it is already inside the polygon and it is "under the new line". |
The last step (4.) is the reason we chose this algorithm over other existing algorithms. Because of its lack of loop for() on every pixel, it is compatible with Eigen library which significantly improves the speed of our code. Which is important, considering the size of the picture we are working with.
|


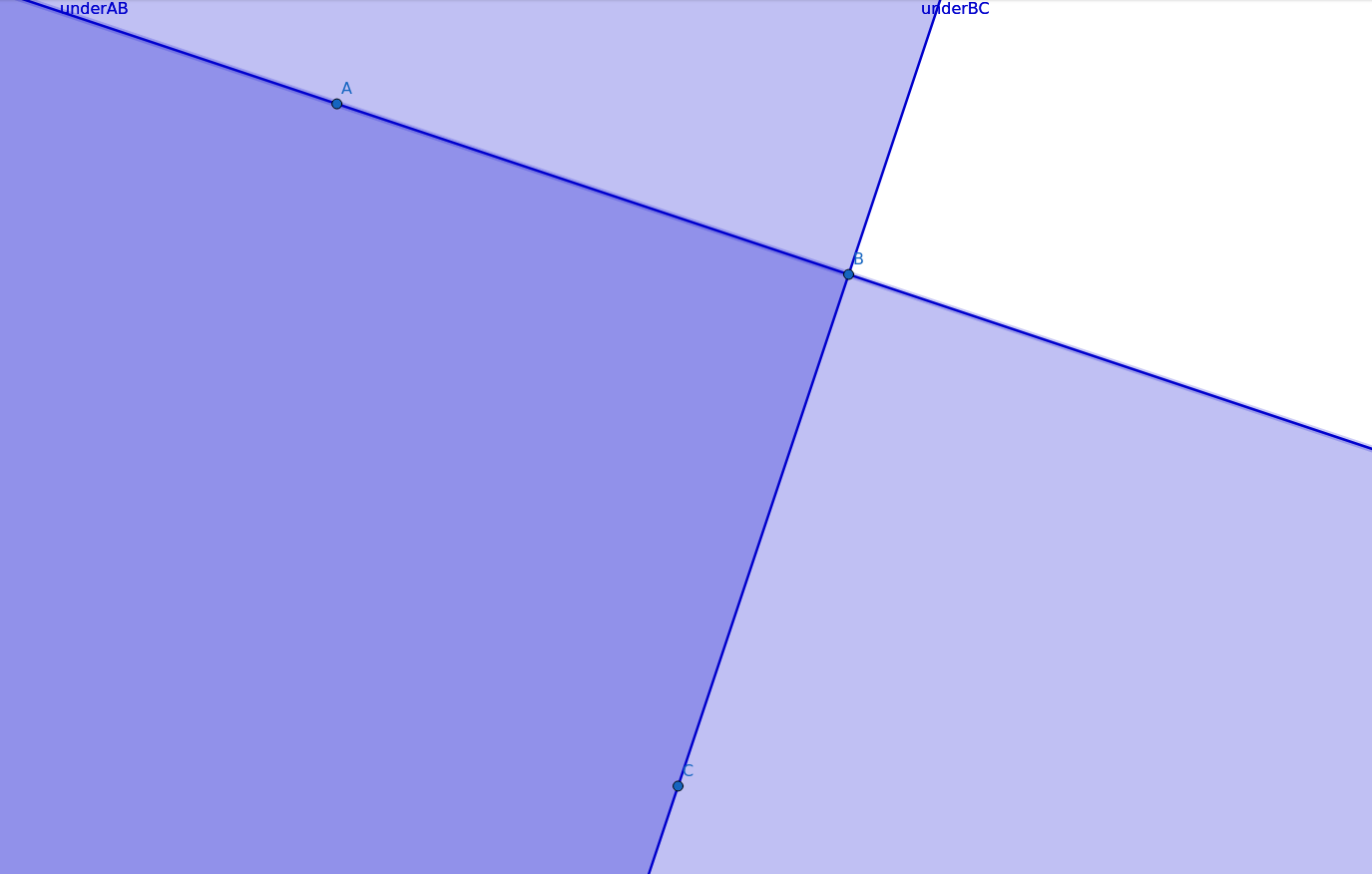

However this algorithm presents some issues :
-
It works only with convex polygons

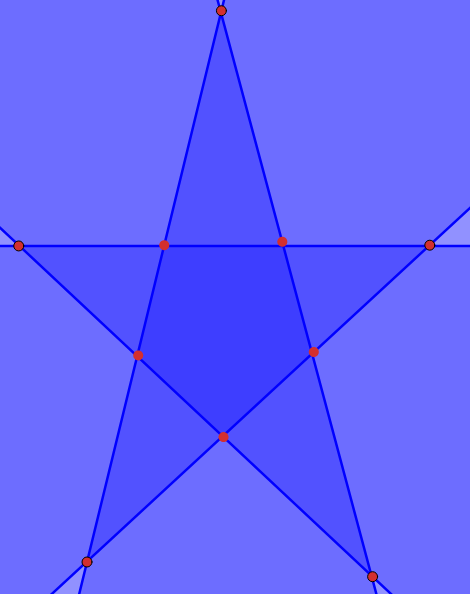
| A simple solution could be to intersect/add multiple convexs polygons |
-
It works only if the set of point is made clockwisely. If the points are written in random order, the selection will be invalid. Worst case scenario being counter-clockwisely, leading to an empty selection
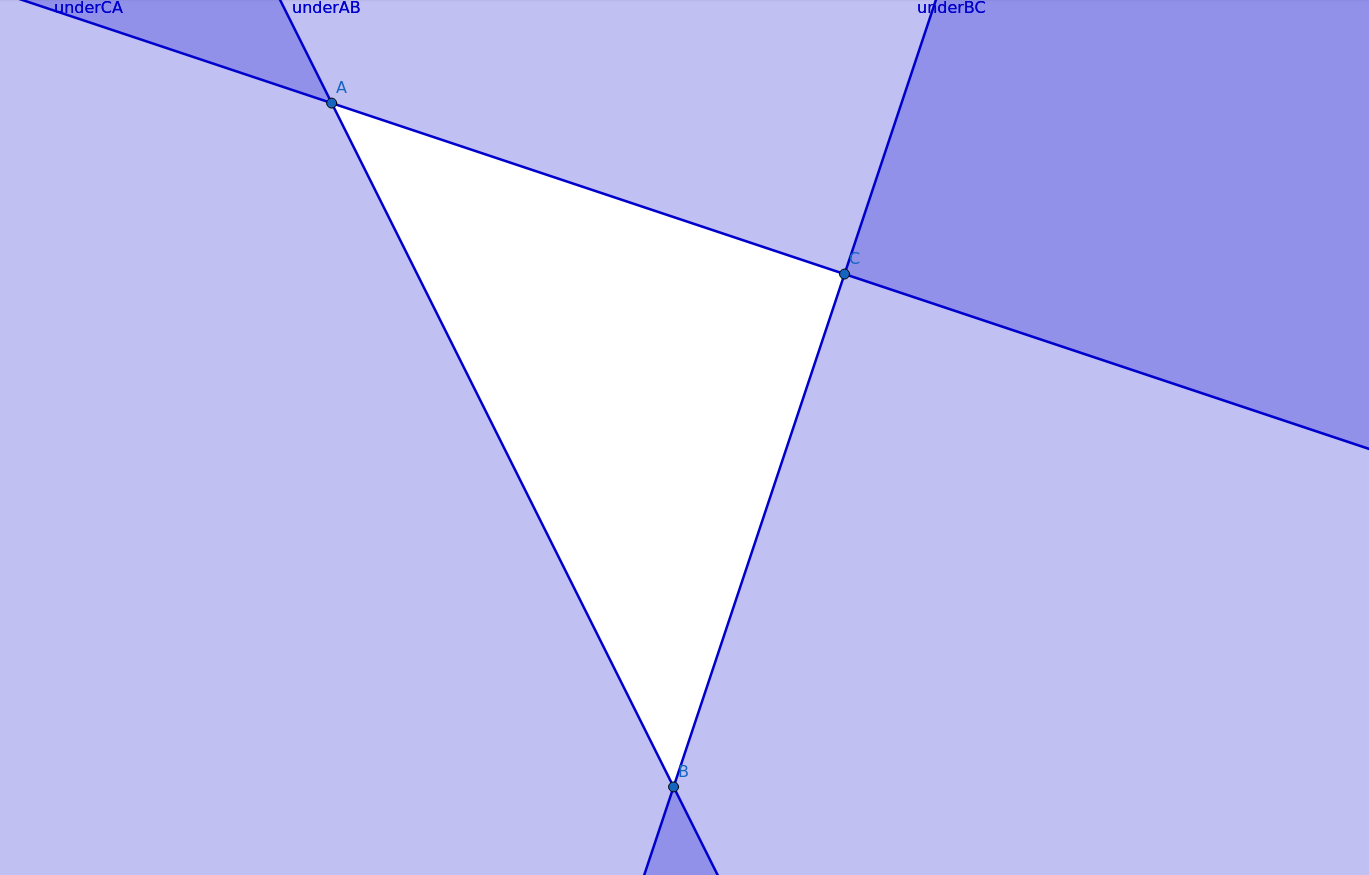
Fortunately, we can easily fix the last case scenario (counter-clockwisely)
[...]
mask_t empty = mask_t::Zero(nrows, ncols); (1)
if ( isInside.array().isApprox( empty.array() ) ) (2)
{
isInside = mask_t::Ones(nrows, ncols);(3)
for (auto it = pointList.begin(); it != pointList.end(); ++it)
{
point_t ptA = (std::next(it)!=pointList.end()) ? *std::next(it) : *pointList.begin();(4)
point_t ptB = *it;
auto xA = ptA.first;
auto yA = ptA.second;
auto xB = ptB.first;
auto yB = ptB.second;
auto a = yA-yB;
auto b = xB-xA;
auto c = a*xA + b*yA;
isInside = ( isInside && ((x.array()*a + y.array()*b) <= c) );
}
}
return isInside;
}; //end of computeMask()| 1 | Creating an empty mask for reference |
| 2 | If the mask is empty, there’s a chance it’s because points were entered in the wrong order |
| 3 | If so we need to reset the mask because it is now empty and we would intersect on an empty mask |
| 4 | And we just invert the definition of pointA and pointB which will cause the inversion of oriented lines |
| With this additionnal feature, as long as points are written turning around de polygon, it doesn’t matter which way you’re turning around the polygon. However points in random order will lead to bad results. |