Eye2Brain methods

1. Hybridazable Discontinuous Galerkin

One of the biggest issue in biological computation, in particular for small systems, is the high accuracy that all the models require to be able to reproduce physiological behaviors. To figure out this point we decided to adopt the Hybridizable Discontinuous Galerkin (HDG) method [Cockburn2009].

With our group we elaborated from a theoretical viewpoint Integral Boundary Conditions (IBC) for HDG, a new feature in the numerical analysis world. The great advantages of HDG are: - the equation are enforce element-by-element leading to locally conservative property - optimal convergence properties - high accuracy for both primal and dual variables.

One of the main controversy is the high computational cost that we have settled adopting static condensation. A detailed explanation of all the features we have developed is in REFERENCE TO THE HDG PART OF THE DOC and within a paper in preparation [HDGinprep].

2. Coupling 3D-0D

The other big issue in the context of biomathematics is the choice of the region of interest and consequently the boundary conditions (BCs).

In order to avoid artificial abnormalities due to bad selection of BCs, especially for hemodynamics, we have decided to couple the region of interest that is described with a three-dimensional geometry, with the characterization of the blood circulation in the back of the eye with a lumped parameter approach. In this way, we are maintaining the closed-loop characteristic of the blood circulation without increasing in an exceeding way the computational effort.

The problematic introduced by this 3D-0D coupling is mainly due to the instabilities of numerical methods or again the computational cost. To figure out the issues for our problem, we decided to adopt an operator splitting method inspired by the work of [Glowinski2003][Carichino2018]. This operator splitting method preserves the energy of the system and provides two decoupled subsystems that are easier to deal with than the original monolithic system. The version we have adopted at this stage of the work is a first order convergence in time (Fig. 1).

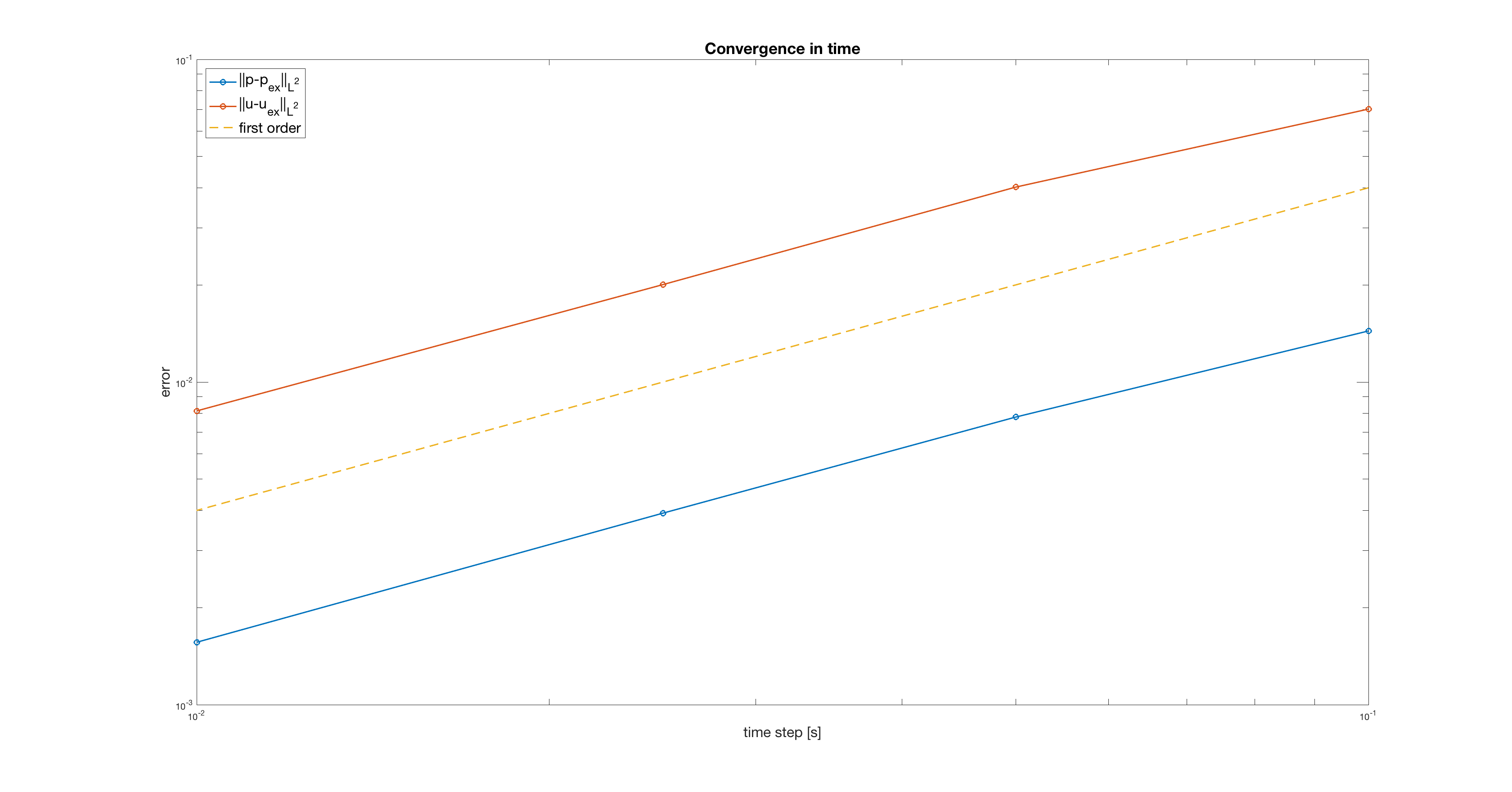
Convergence rate of pressure and flux of the operator splitting

Figure 1: pressure and flux convergence graph in time of the 3D-0D operator splitting.

This novel operator splitting method has been presented by the group at the Congres National d’Analyse Numerique in May 2018 [SalaCANUM2018].

Bibliography

References

  • B. Cockburn, J. Gopalakrishnan, and R.o Lazarov. Unified hybridization of discontinuous galerkin, mixed, and continuous galerkin methods for second order elliptic problems. SIAM Journal on Numerical Analysis, 47(2):1319{1365, 2009.

  • L. Sala, R. Hild, C. Prud’homme, D. Prada, S. Bertoluzza, R. Sacco, C. Trophime, M. Szopos, and G. Guidoboni. An implementation of HDG methods with Feel++. Application to problems with integral boundary condition. In preparation.

  • R. Glowinski. Finite element methods for incompressible viscous flow. Handbook of numerical analysis, 9:3{1176, 2003.

  • L. Carichino, G. Guidoboni, and M. Szopos. Energy-based operator splitting approach for the time discretization of coupled systems of partial and ordinary differential equations for fluid flows: The stokes case. Journal of Computational Physics, 364:235{256, 2018.

  • L. Sala, C. Prud’Homme, G. Guidoboni, and M. Szopos. Unconditionally stable operator splitting method for a multiscale application in ophthalmology. Congres National d’Analyse Numerique. May 2018.