Thermal Comfort
1. Definition
Thermal comfort has been defined by Hensen as a state in which there are no driving impulses to correct the environment by the behaviour. The American Society of Heating, Refrigerating and Air-Conditioning Engineers ASHRAE defined it as the condition of the mind in which satisfaction is expressed with the thermal environment. According to these definitions, comfort is not a state condition, but rather a state of mind.
2. Elements affecting the thermal comfort
Thermal comfort is caracterised by interaction mechanisms between the environment and the human body and implies the consideration of physical, physiological and psychological aspects.
2.1. Physical aspects
If we consider the ability of the human body to maintain a constant temperature (homeothermic propert), around \( 37 ^{\circ}C\), we consider that the human body is in constant search of equilibrium with the its environment. From a thermodynamic point of view, the human body can be considered as a system in equilibrium with the surrounding environment. This implies heat and mass production, exchanges (gains and losses) with the surrounding environment through different modes of heat (conduction, convection, radiation) and mass (evaporation, respiration) transfers. All of these exchanges can then be transcribed into a balance equation for the human body:
where:
-
\( \mathrm{S} ~ [\mathrm{W}/\mathrm{m}^2\)] is the heat stored by the human body.
-
\( \mathrm{M} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the metabolic heat production.
-
\( \mathrm{W} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the accomplished external mechanical work.
-
\( \mathrm{R} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the heat exchanged between the skin and the environment by radiation.
-
\( \mathrm{C} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the heat exchanged between the skin and the environment by convection.
-
\( \mathrm{K} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the heat exchanged between the skin and the environment by conduction. It concerns only a small part of the human body (part that is in direct contact with a surface).
-
\( \mathrm{E_{sk}} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the latent heat exchanged through the skin.
-
\( \mathrm{E_{res}} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the latent heat exchanged through breathing.
-
\( \mathrm{C_{res}} ~ [ \mathrm{W}/\mathrm{m}^2 \)] is the heat eschanged by convection during breathing.
For a thermal equilibrium, the balance equation cancels \( \left( \mathrm{S}=0\right)\). Thus, the heat produced by the body (metabolism) is dissipated to the environment through the breathing as sensible and latent heat and from the skin or through clothing (fig. 1).
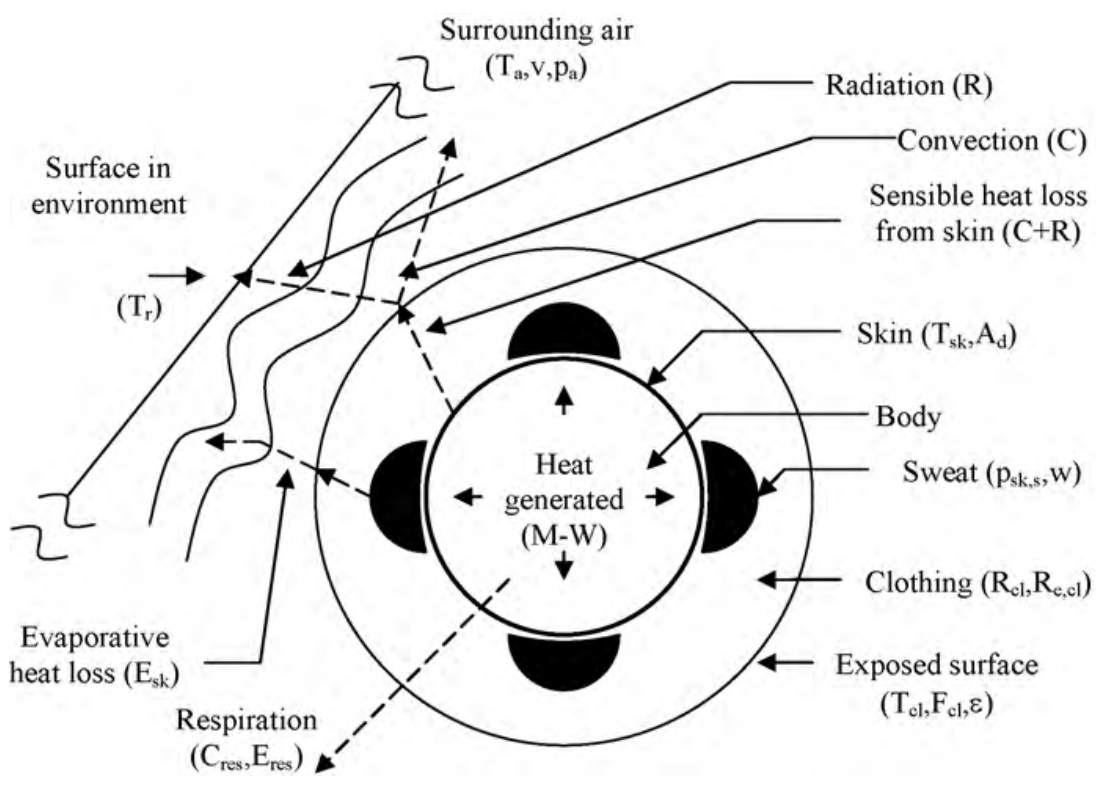
2.1.1. Metabolic production
The metabolic production depends on several factors including the morphology, the activity and the posture of the person. The metabolic production can be estimated from Candas formula [Candas2000] :
where
-
\( \text{M}_\text{b} [\text{W}/\text{m}^2 \)] is the basal or minimal metabolic heat(nude body lying down in the case of thermoneutrality), \( \text{M}_\text{b} = 45 ~ \text{W}/\text{m}^2\).
-
\( \text{M}_\text{p} [\text{W}/\text{m}^2 \)] is the metabolic heat of posture whose values are given in Table 1.
-
\( \text{M}_\text{a} [\text{W}/\text{m}^2 \)] is the metabolic heat of activity whose values are given in Table 2 (the values are given in \( [ \text{w}/\text{m}^2 \)]).
Posture |
||||
Sitting |
Squatting /crouching |
standing up |
Standing up bent or perched |
|
\( \text{M}_\text{p} ~ [\text{W}/\text{m}^2\)] |
10 |
20 |
25 |
30 |
Work |
|||
Light |
Mean |
Heavy |
|
Hands |
10-22 |
22-34 |
34-46 |
One arm |
25-45 |
45-65 |
65-85 |
Two arms |
55-75 |
75-95 |
95-115 |
Body |
95-155 |
155-230 |
230-330 |
2.1.2. Clothing effects
Clothing is an important factor in achieving thermal comfort at different temperatures. The insulation effect of clothes is expressed in "clo" where \( 1 \text{clo} = 0.155 \text{m}^2 \text{K}/\text{W}\):
-
\( \text{clo} = 0 \) corresponds to a naked person.
-
\( \text{clo} = 1 \) corresponds to the insulating value of clothing needed to maintain a person in comfort sitting at rest, in a room at \( 21^{\circ}\text{C} \) with air movement of \( 0.1 \text{m}/\text{s} \) and relative humidity less than \( 50 \%\) (typically a person wearing a business suit).
As it is not practical to directly measure clothing insulation, values from tables that have been developed from clothing insulation studies are usually used (see Table 3 for an example). The insulation of a clothing ensemble can be evaluated from the following formula:
where
-
\( I_{cl} ~ [\text{clo}\)] is the insulation of the entire ensemble.
-
\( I_{clu,i} ~ [\text{clo}\)] is the effective insulation of the clothing garment \( i\).
The typical values of \( I_{cl} \) considered for an office environnement are \( 0.5 ~ \text{clo}\) in summer and \( 1.0 ~ \text{clo}\) in winter.
Cloth |
\( I_{cl} ~ [\text{clo}\) ] |
Briefs |
0.04 |
Shoes |
0.02 |
socks |
0.03 |
Short sleeve shirt |
0.19 |
Straight trousers |
0.15 |
Total |
0.43 |
The clothing area factor taking into account the effects of radiation and convection is evaluated from the following formula formula:
where
-
\( h_c ~ [ \text{W} / \text{m}^2 \) ] is the convective heat transfer coefficient.
-
\( h_r ~ [ \text{W} / \text{m}^2\) ] is the radiatif heat transfer coefficient.
It can also be evaluted from the following:
where
-
\( A_{d,cl} ~ [\text{m}^2\)] is the Dubois surface area of nude body
-
\( A_{d} ~ [\text{m}^2\)] is the Dubois surface area of clothed body. It is given by:
where \( m ~ [\text{m}^2\)] is the body mass and \( l ~ [\text{m}\)] is the body height.
2.1.3. Conductive effect
Even if the human body exchanges heat by conduction (K), only small body surface is concerned. When a great body area is in contact for example with furniture, thermal equilibrium rapidly occurs. The body area in contact with the furniture behaves as an insulating toward the environment. Generally in the steady state, the bodies' temperatures and the conductive effects are neglected; rather they are included into the convective exchanges.
2.1.4. Convective effect
The global convective heat flux \( \text{C}\) exchanged between the human body and its environment is:
where:
-
\( T_a ~ [ \text{K} \)] is the ambiant air temperature.
-
\( T_{sk} ~ [ \text{K} \)] is the mean skin temperature.
-
\( A_c ~ [ \text{m}^2 \)] is the effective convection area of the body (almost taken to be equal to the Dubois area \( A_d\)).
-
\( f_{cl}~ [ - \)] is the clothing area factor.
-
\( h_c ~ [ \text{W}/ \left( \text{m}^2 \text{K}\right) \)] is the convective heat coeffient. It is given by:
where \( v_a\) is the air velocity, \( v_{ar}\) is the resultant air velocity taking into account the ambient air velocity and that due to activities and displacements of the person:
M is the above mentioned metabolic heat production, with the supplementary condition \( \text{M} = 200 ~ \text{W}/\text{m}^2\) when M is found greater than \( 200 ~ \text{W}/\text{m}^2\) so that to limit convective effect C to 0.7.
2.1.5. Radiative effect
The radiative heat lost from the skin \(\text{R}\) is given by:
where:
-
\( h_r\) is the radiative heat transfer coefficient.
-
\(T_{mr}\) is the mean radiant temperature.
-
\(T_{sk}\) is the mean skin temperature.
-
\( A_r\) is the effective radiation area of the body,
-
\( f_{cl}\) is the clothing area factor.
The radiative heat transfer coefficient \( h_r \) is given by:
where:
-
\( \sigma = 5.67 \times 10^8 \text{W}/ \text{m}^2 \text{K}^4 \) is the Stefan-Boltzmann coefficient.
-
\( \varepsilon_{sk} = 0.97 \) is the emissivity of the skin.
-
The effective radiation area of the body (\( A_r\)) can be written as:
with \(\frac{A_r}{A_d}=\begin{cases}0.67 & \text{for a squatting person}, \\ 0.70 & \text{for a sitting person,} \\ 0.77 & \text{for a standing person.} \end{cases}\)
Mean radiant temperature
The mean radiant temperature is defined as the uniform temperature of an imaginary enclosure in which the radiant heat transfer from the human body is equal to the radiant heat transfer in the actual non-uniform enclosure. It is estimated from the temperature of the surrounding surfaces weighted according to their relative influence on a person by the view factor :
where
-
\(T_i\) [\(\,^{\circ} \text{C}\)] is the temperature of the surface \(i\).
-
\(F_{p-i}\) is the view factor between the person and the surface \(i\), \(\sum\limits_{i=1}^{n} F_{p-i} = 1\).
-
\(n\) is the total numbe rof the surrounding surfaces.
| Model for the computation of the view factors are under development and not yet implemented, see Radiative Heat Transfer. |
Cannistraro et al. proposed a simple algorithm for the calculation of the view factors between human body and rectangular surfaces in parallelepiped environments :
where:
-
\(a\) [m] is the width of the analysed surface
-
\(b\) [m] is the height of the analysed surface
-
\(c\) [m] is the distance between the person and the analysed surface
-
\(F_\mathrm{max}, \, A, \, C, \, D \, \text{and} \, E \) are constants determined by Cannistraro et al. for different postures and positions of the person regarding the surface . For instance, for seated person and vertical rectangle in front of the him and above his centre, or behind him and below his centre, \(F_\mathrm{max} = 0.132\), \(A = 1.14505\), \(B = 0.14524\), \(C = 0.74379\), \(D = 0.10312\) and \(E = 0.02967\).
The mean radiant temperature can also be experimentally estimated from globe measurement. In forced convection conditions, the following formula is usually used [ISO-7730] :
where:
-
\(T_{mr}\) [\(\,^{\circ} \text{C}\)] is the mean radiant temperature.
-
\(T_g\) [\(\,^{\circ} \text{C}\)] is the globe temperature.
-
\(T_a\) [\(\,^{\circ} \text{C}\)] is the air temperature.
-
\(v_a\) [m/s] is the air velovity at the level of the globe.
-
\(\varepsilon\) [-] is the emissivity of the globe.
-
\(D\) [m] is the diameter of the globe.
2.1.6. Sensible heat loss from the skin
Sensible heat exchange from skin surface to a surrounding environment must pass through clothing. Both convective and radiative heat losses from the outer surface of a clothed body can be expressed in terms of a heat transfer coefficient and the difference between the mean temperature of the outer surface of the clothed body and an appropriate environmental temperature:
-
Convective loss
-
Radiative loss
The coefficients \( h_c\) and \( h_r\) are both evaluated at the clothing surface.The convective and raditive effects are commonly combined to describe the total sensible:
where \( T_0 ~ [\text{K} \) ] is the operative temperature: the uniform temperature of an imaginary black enclosure in which an occupant would exchange the same amount of heat by radiation plus convection as in the actual non-uniform environment.
Based on the above relation, the operative temperature \( T_O\), can be defined as the average of the mean radiant and the ambient air temperatures, weighted by their respective heat transfer coefficients. For occupants engaged in near sedentary physical activity (with metabolic rates between \( 1.0 ~ \text{met}\) and \( 1.3 ~ \text{met}\)), not in direct sunlight, and not exposed to air velocities greater than \( 0.20 ~ \text{m}/\text{s}\), the relationship can be approximated by:
where \( T_{mr} \) is the mean radiant temperature and \( T_a\) is the ambient air temperature.
The actual transport of sensible heat passing through clothing involves conduction, convection, and radiation. It is usually convenient to combine these into a single thermal resistance of clothing \( I_{cl}\):
with \( h = h_c + h_r \).
2.1.7. Evaporative heat loss from the skin
The evaporative heat loss from skin \( E_{sk}\), depends on the amount of moisture on skin (\( w\)), and the difference between the water vapour pressure at skin surface (\( p_{sk,s}\)), and that in the ambient environment (\( p_a\)):
where
-
\( R_{e,cl} ~ [ \text{m}^2 \text{kPa} / \text{W} \)] is the evaporative resistance of clothing.
-
\( h_{e} ~ [ \text{W} / \text{m}^2 \text{K} \)] is the evaporative heat transfer coefficient.
2.1.8. Heat loss due to breathing
Respiratory heat loss is often expressed in terms of sensible heat loss \( \text{C}_{res} \), and latent heat loss \( \text{E}_{res} \). Sensible and latent heat losses are relatively small and can be estimated from:
2.1.9. Net heat production of the human body
The net heat production in the human body \( \text{M}-\text{W} \) is either stored (S), causing the body’s temperature to rise, or dissipated to the environment through skin surface and respiratory trac. Therefore, the heat balance for a human body reads:
-
The rate of heat storage in the body \( \left(\mathrm{S} \right) \) can be written separately for each compartment (a human body can be considered as consisting of two concentric thermal compartments: the skin and the core) in terms of thermal capacity and change rate of temperature as follows:
where
-
The subscipts \( cr\) and \( sk\) refer to the core and the skin copartments resepectivly.
-
\( \mathrm{S}~ [ \text{W}/\text{m}^2\)] is the heat storage
-
\( \alpha_{sk} ~ [ - \)] is the fraction of total body mass concentrated in skin compartment.
-
\( m ~ [ \text{kg} \)] is the body mass
-
\( c_{p,b} ~ [ \text{J} / \left(\text{kg} \text{ K} \right)\) ] is the specific heat of body tissue.
-
\( T ~ [ \text{K} \)] is the temperature.
-
\( A_d ~ [ \text{m}^2 \)] is the Dubois surface area of nude body.
2.2. Physiological aspect
The physiological aspect in the study of thermal comfort concerns the homeothermic property which is ensured by the thermoregulation system of the human body. The energy produced by the metabolism of the human body is continuously dissipated and controlled through the exchanges described above in order to maintain a constant body temperature. The control temperature in the human brain (hypothalamus) varies from \( 36.8 ^{\circ} \text{C} \) (for resting activity) to \( 37.9 ^{\circ} \text{C} \) (for high activity). In contrast, the skin temperature varies from \( 29^{\circ} \text{C} \) to \( 35^{\circ} \text{C} \) (depending on the part of the body), it is inversely proportional to activity (skin temperature decreases with increasing activity).
2.3. Psychological aspect
The psychological aspects of thermal comfort are strongly related to the physical and physiological aspects mentioned above. They are mainly related to the subjective character (sensation) of the human being regarding his environment. The concept of thermal sensation can have several definitions which can lead to confusion on the way it is evaluated but also on the way is correlated with the physical parameters of comfort (mainly temperature). When it comes to evaluating a thermal environment by physical measurements, comfort is expressed with acceptable temperature ranges, an optimal comfort temperature, a neutral temperature, or comfort scales such as ASHRAE or Bedford scales:
Bedford scale |
ASHRAE scale |
7: Much too hot |
+3: Hot |
6: Too warm |
+2: Warm |
5: Comfortably warm |
+1: Slightly warm |
4: Comfortable |
0: Neutral |
3: Comfortably cold |
-1: Slightly cool |
2: Too cold |
-2: Cool |
1: Much too cold |
-3: Cold |
3. Thermal comfort approches
At present, two different approaches for the definition of thermal comfort coexist, each one with its potentialities and limits: the rational or heat-balance approach and the adaptive approach. The rational approach uses data from climate chamber studies to support its theory, best characterized by the works of Fanger while the adaptive approach uses data from field studies of people in building. Herein, only the rational approach is described. For more details on the adaptive approach refer to Djongyang et al..
3.1. The rational or heat-balance approach
The heat-balance approach is based on Fanger’s experiments [10] in controlled climate chamber on 1296 young Danish students, using a steady-state heat transfer model. In these studies, participants were dressed in standardised clothing and completed standardised activities, while exposed to different thermal environments. In some studies the thermal conditions were chosen, and participants recorded how hot or cold they felt, using the seven-point ASHRAE thermal sensation scale (Table 1). In other studies, participants controlled the thermal environment themselves, adjusting the temperature until they felt thermally "neutral" [19]. Fanger’s model combines the theories of heat balance with the physiology of thermoregulation to determine a range of comfort temperatures which occupants of buildings will find comfortable. From his investigatons, Fanger developed linear relationships between activity level and sweat rate and between activity level and mean skin temperature. After substituting these two linear relationships into heat balance equations, a "comfort equation" was obtained. That comfort equation was expanded using data from 1296 participants. The resulting equation described thermal comfort as the imbalance between the actual heat flow from the body in a given thermal environment and the heat flow required for optimum (i.e. neutral) comfort for a given activity. This expanded equation related thermal conditions to the seven-point ASHRAE thermal sensation scale, and became known as the "Predicted Mean Vote" (PMV) index. The PMV was then incorporated into the "Predicted Percentage of Dissatisfied" (PPD) index.
4. Predicted Mean Vote (PMV)
The PMV index suggested by Fanger predicts the mean response of a large group of people according to the ASHRAE thermal sensation scale. Subjects exposed to the climate chambers are asked to give their opinions according to the ASHRAE seven-point scale of thermal sensation. A mean vote (MV) is obtained for a given condition by finding the mean value of the feeling given by all the subjects for that condition. Fanger related PMV to the imbalance between the actual heat flow from a human body in a given environment and the heat flow required for optimum comfort at a specified activity by the following equation:
where \( \text{M}\) is the metabolic rate and \( \text{L}\) is the thermal load on the body, defined as the difference between internal heat production and heat loss to the environment for a person hypothetically kept at comfort values of the skin temperature and heat loss through sweating at the activity level.
As it is based on the ASHRAE thermal senstion scale, PMV goes from -3, when the occupants are cold, to +3 when the occupants are hot. The best value is 0 when an occupant’s internal heat production is the same as its heat loss (thermal equilibrium between the ocuupant and his environment). The figure above shows this scale, the best case is to be in the green part.

This balance can be influenced by many factors :
-
Physical activity
-
Clothing of the individual
-
Parameters of the thermal environment (ventilation, …)
This formula can estimate the PMV :
With :
-
\(T_{cl}=35.7-0.028\,(M-W)-I_{cl}\{ 3.96 \cdot 10^{-8}\cdot f_{cl}\,\left((T_{cl}+273)^4-(T_{mr}+273)^4\right)+f_{cl}\cdot h_{c}\,(T_{cl}-T_a)\}\)
-
\(h_c=\begin{cases}2.38\cdot|T_{cl}-T_a|^{0.25}&\text{for}& 2.38\cdot|T_{cl}-T_a|^{0.25}\geqslant 12.1\sqrt{v_{ar}} \\12.1\sqrt{v_{ar}}&\text{for}&2.38\cdot|T_{cl}-T_a|^{0.25}<12.1\sqrt{v_{ar}}\end{cases}\)
-
\(f_{cl}=\begin{cases}1.00+1.290 I_{cl} &\text{for}& I_{cl}\leqslant 0.078 \,\text{m}^2\text{K}/\text{W}\\ 1.05+0.645 I_{cl} &\text{for}& I_{cl}>0.078 \,\text{m}^2\text{K}/\text{W} \end{cases}\)
Where :
-
\(M\) [\(\text{W}/\text{m}^2\)] is the metabolic rate
-
\(W\) [\(\text{W}/\text{m}^2\)] is the effective mechanical power. In most types of industrial work, it is so small that it is assumed to be nil.
-
\(I_{cl}\) [\(\text{m}^2\text{K}/\text{W}\)] is the clothing insulation
-
\(f_{cl}\) [–] is the clothing surface area factor
-
\(T_a\) [°C] is the air temperature
-
\(T_{mr}\) [°C] is the mean radiant temperature
-
\(v_{ar}\) [m/s] is the relative air velocity
-
\(p_a\) [Pa] is the water vapor partial pressure
-
\(h_c\) [\(\text{W}\,\text{m}^{-2}\text{K}^{-1}\)] is the convective heat transfer coefficient
-
\(T_{cl}\) [°C] is the clothing surface temperature
| \(M-W\) corresponds to the net metabolic heat production |
5. Predicted Percentage of Dissatisfied (PPD)
This index gives a quantitative prediction of the percentage of thermally dissatisfied people. The PPD is given by this formula :
This figure represents the function :
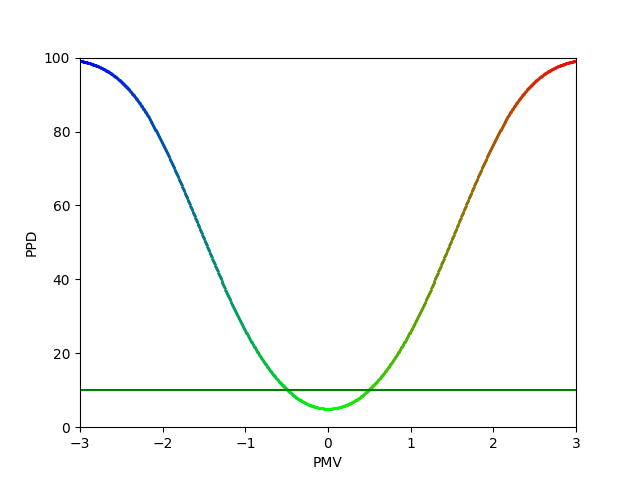
We can see that even if the PMV is null, the PDD has a value of 5%.
The recommended thermal limit in the norm [ISO-7730] on the PMV scale is between -0.5 and 0.5. It corresponds to as PDD lesser than 10%, represented by the green horizontal line in the figure above.
References
-
[Allab17] Allab, Yacine. Building ventilation performance assessement : ventilation efficiency and thermal comforT. PhD thesis, École nationale supérieure d’arts et métiers, 2017
-
[ASHRAE2004] ANSI/ASHRAE Standard 55. Thermal Environment Conditions for Human Occupancy, 2004.
-
[Candas2000] Candas, V., Traité Génie énergeétique, Techniques de l’Ingénieur, Doc. BE 9 085, 2000.
-
[Cannistraro1992] Cannistraro, G., Franzitta, G., and Giaconia, C., Algorithms for the calculation of the view factors between human body and rectangular surfaces in parallelepiped environments, Energy and Buildings, 19(1992) 51-60
-
[Djongyang2010] Djongyang, N., Tchinda, R., and Njomo, D. Thermal comfort: A review paper, Renewable and Sustainable Energy Reviews 14 (2010) 2626–2640.
-
[Gilani2015] Syed Ihtsham ul Haq Gilani, Muhammad Hammad Khan and William Pao, Thermal comfort analysis of PMV model Prediction in Air conditioned and Naturally Ventilated Buildings,2015.
-
[Hensen1991] Hensen J. L. M., On the thermal interaction of building structure and heating and ventilating system, PhD thesis, Technische Universiteit Eindhoven; 1991. Download PDF
-
[ISO-7730] Ergonomics of the thermal environment — Analytical determination and interpretation of thermal comfort using calculation of the PMV and PPD indices and local thermal comfort criteria
-
[Sarah2015] Sarah Benharkat and Djamila Rouag-Saffidine, Approche adaptative du confort thermique dans les espaces d’enseignement universitaire à Constantine,2015