Moisture transfer
1. Introduction
Water is one of the main causes of deterioration of building materials and, therefore, of building structures. Whatever its physical form (solid, liquid, vapor), it may be behind serious damages of the different building parts and imperil the normal behavior of the entire building. For instance, liquid water is involved in several physico-chemical reactions such as concrete carbonation or steel corrosion and can significantly reduce the mechanical resistance of the whole structure. Vapor and liquid water may also decrease the thermal performance of insulating materials, contribute to the development of mold and thus negatively impact the interior air quality and thermal comfort.
2. Moisture sources in building
Moisture may reach buildings in liquid or vapor formes and come from different sources:
-
Liquid water may come from precipitation (rain and melting snow), plumbing leaks, adjoining soil or be found as built-in water in some construction materials such as concrete and wooden materials.
-
Water vapor also may come from adjacent soil or be found as built-in vapor in some construction materials. In addition water vapor may come from exterior air or result from human activity and other processes within the building Straube.
3. Moisture related problems in buildings
Moisture may be involved in several problems in building :
-
Thermal comfort : depending on the relative humidity of the ambient air, a given temperature may be tolerated or not by the human body. For example, if the air temperature is around \( 22^{\circ} \text{C} \), the relative humidity must be around \(50\%\) \(45\%\) to \(65\%\). In general, the relative humidity in the building inclosure must vary between 30% to 70% to ensure the thermal comfort of the occupants.
-
Health problems : Too dry air \( <30 \% \) enables the development of bacteria and viruses, respiratory infections, asthma, … Too moist air \( >70 \% \) combined with high temperature enables the development of bacteria, moths, dust mites and micro-fungi that can also be responsible for several respiratory illnesses.
-
Building damages : liquid water as well as water vapor can cause serious damages to buildings and lead to their destruction if no precautions are taken. The most frequent building damages caused by moisture are :
-
Visual aspect damage: mold growth, swelling, paint fading, delamination, …
-
Mechanical properties: in some porous materials, water may be involved in several physico-chemical reactions such as electrocorrosion and thus lead to severe mechanical resistance reduction. In hygroscopic materials such as wood, in addition to aspect changings such as swelling, moisture enables the growth of micro-organisms that can also result in mechanical resistance reduction.
-
Thermal properties: in porous media, moisture replaces the air contained in the voids and thus increases the material thermal conductivity. As insulating materials are of low density, the void proportion suceptible to be filled with moisture is important. This property, that gives the insulating materials their thermal properties, makes them sensitive to moisture. This thermal conductivity modification increases heat flow through the insulating materials and thus the energy consumption of the building.
-
4. Moisture transfer modes
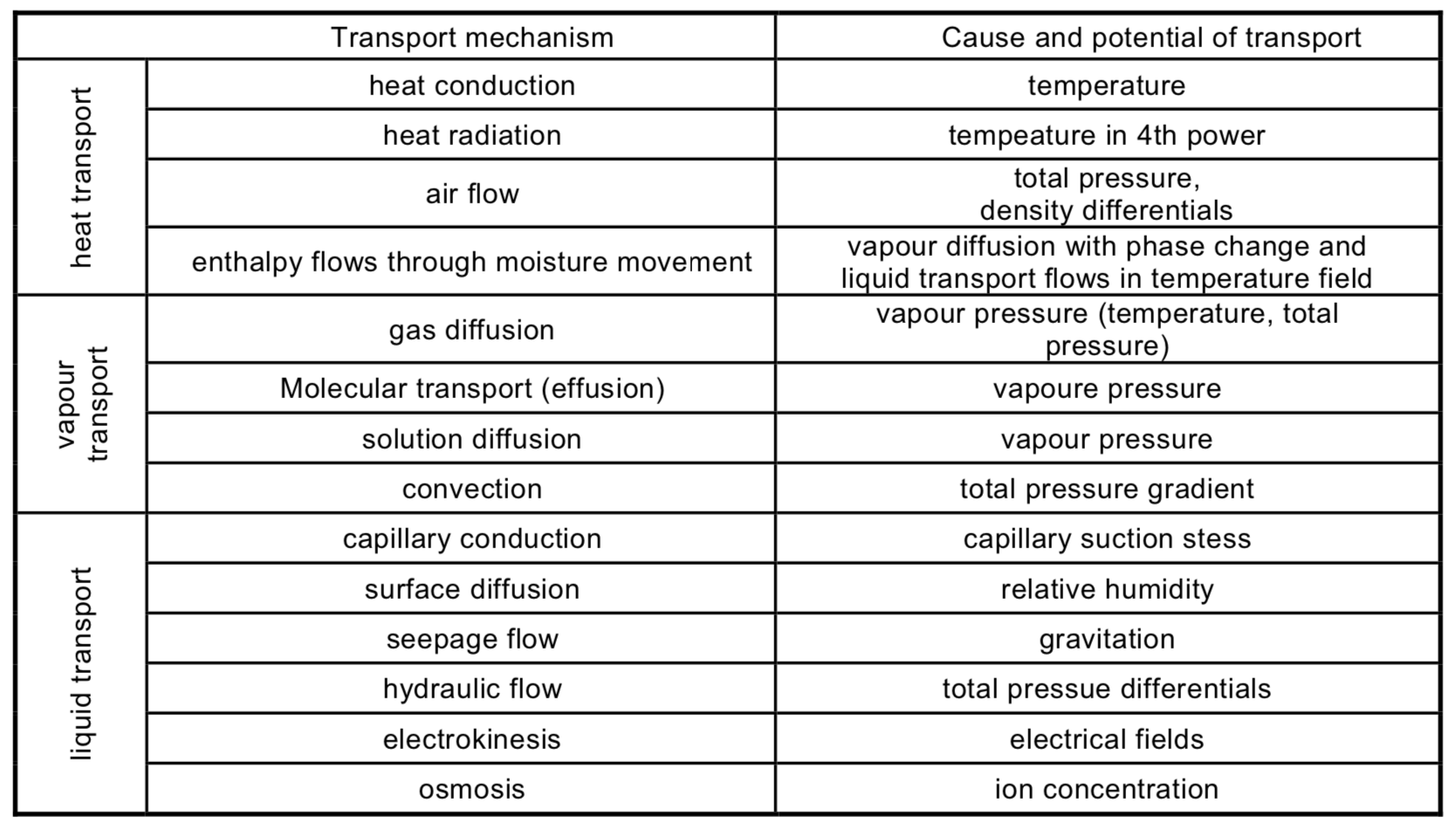
Moisture transfer can occur through a porous media in all four states: vapor, liquid, solid and adsorbed water. In vapor and liquid, water molecules are more mobile than in the latter two, and the first two processes may significantly dominate the other two in most cases Kumaran. Herein only the two first processes are taken considered:
4.1. Vapor transport
According to the kinetic gas theory, water vapor transport is driven by three diffusion potentials: the mass fraction, the temperature and the total pressure Künzel. In building physics, total pressure and temperature gradients driven diffusion can be neglected. Vapor diffusion due to mass fraction gradient acts to move water vapor through the air within porous media from high to low vapor concentration. It is called Fick’s diffusion and can be described by the Fick’s law.
4.2. Liquid transport
Liquid water transport in porous media occurs mainly through capillary suction. Capillary suction moves liquid moisture slowly and steadily through porous materials from regions of high liquid concentration to regions of low concentration Straube. Its driving gradient is the suction stress or the relative humidity Künzel.
4.3. Moisture storage
In addition to allow vapor and liquid moisture transfer, most construction materials are hygroscopic, which means that they can store water vapor. The amount of moisture that can be stored by a porous material is proportional to its moisture storage capacity \(\xi\).
For the moisture transfer to occure, four conditions must be met:
-
A moisture source is available
-
A mean for moisture transport is available (pores)
-
A driving force (moisture gradient, pressure gradient, …)
-
The material is sensitive to moisture damage.
In theory, removing one of these conditions would lead to prevent moisture transfer but this is not realistic. Indeed, moisture sources and driving forces can not be removed, moisture would always find its way through the smallest defaults even when all precautions were taken, and using only materials that are not sensitive to moisture would be too expensive. The most relevent way to prevent moisture damage in buildings is design optimization and moisture control. This is acheived using moisture transfer models. In building energy analysis, moisture and heat transfers take place simultaneously and are affected by each other, coupled heat and moisture transfer models are then needed to conduct building energy performance analysis and comfort studies.
5. Moisture transfer models
Each moisture transfer mechanism is described by an equation that takes the following form Kumaran:
where
-
\(j_B\) is the rate at which the quantity \(B\) is transported
-
\(k\) is a transport coefficient that caracterizes the medium through which the transport occurs.
-
\(\mathrm{grad}\,\phi_B\) is a driving potentiel
5.1. Vapor transport
In building physics, it is assumed that vapor transport occurs mainly through diffusion, driven by the mass fraction potential and known as Fick’s law. According to the ideal gas law, mass fraction is proportional to partial pressure. The Fick’s law can then be expressed according to the partial pressure potential as follows:
where
-
\(j_v\) [\(kg/(m^2.s)\)] is the vapor flux density
-
\(\delta_p\) [\(kg/(m.s.Pa)\)] is the water vapor permeability of the building material
-
\(p_v\) [\(Pa\)] is the water vapor partial pressure
5.2. Liquid transport
Liquid water transport within building materials is mainly due to capillary suction and can be expressed by the following equation:
where
-
\(j_w\) [\(kg/(m^2.s)\)] is the liquid flux density
-
\(D_w\) [\(m^2/s\)] is the capillary transport coefficient
-
\(w\) [\(kg/m^3\)] is the water content
The liquid trnasport equation can also expressed according to the relative humidity \(\phi\) :
with
where
-
\(j_w\) [\(kg/(m^2.s)\)] is the liquid flux density
-
\(D_\phi\) [\(kg/(m.s)\)] is the liquid conduction coefficient of the building material
-
\(D_w\) [\(m^2/s\)] is the capillary transport coefficient
-
\(\xi\) [\(kg/m^3\)] is the moisture storage coefficient of the material
-
\(\phi\) [\(-\)] is the relative humidity
6. Moisture transfer equation
The moisture equations specified in the following clauses contain the following assumptions:
-
constant geometry, no swelling and shrinkage;
-
no chemical reactions are occurring;
-
no change in material properties by damage or ageing;
-
local equilibrium between liquid and vapour without hysteresis;
-
moisture storage function is not dependent on temperature.
-
temperature and barometric pressure gradients do not affect vapour diffusion.
The moisture transfer equation is obtained by writting the mass conservation equation. In porous material, moisture transport is driven by three different potentials: pressure, water content and relative humidity (Table 1). Thus, the moisture transport equation can theorically be expressed according to any of them. However, it can be shown that there is not always a direct connection between the water content and the driving force (the capillary suction stress) for the liquid transport. Furthermore, water content is not continous in all building materials such as multi-layered materials. Its use may lead to wrong estimates. It is then more suitable to use the relative humidity[Künzel1995].
The transient differential equation of moisture tranport in porous material can be expressed according to the relative humidity as follows :
where
-
\(\xi\) [\(\text{kg}/\text{m}^3\)] is the moisture storage capacity of the material
-
\(\phi\) [\(-\)] is the relative humidity
-
\(D_w\) [\(\text{m}^2/\text{s}\)] is the capillary transport coefficient
-
\(\delta_p\) [\(\text{kg}/(\text{m}.\text{s}.\text{Pa})\)] is the water vapor permeability of the building material
-
\(p_\text{sat}\) [\(\text{Pa}\)] is the water vapor saturation pressure
-
\(G\) [\(\text{kg\text{/(\text{m}^3.s)\)] is a moisture source
with
References
-
[CEN2007] EN 15026, Hygrothermal performance of building components and building elements - Assessment of moisture transfer by numerical simulation, CEN, 2007.
-
[HAM2002] C.-E. Hagentoft, HAMSTAD – Final report: methodology of HAM-modeling, Report R-02:8, Gothenburg, Department of Building Physics, Chalmers University of Technology, 2002.
-
[Kumaran1994] Kumaran, M. K., Mitalas, G. P. and Bomberg, M. T. (1994), 'Fundamentals of transport andstorage of moisture in building materials and components', Trechsel, H. R. (ed), Moisture control in buildings.
-
[KUN1995] Künzel H, Simultaneous Heat and Moisture Transport in Building Components, PhD thesis, Fraunhofer Institute of Building Physics, 1995.
-
[Kunzel2004] Kunzel, H.M., Holm, A., Zirkelbach, D. and Karagiozis, A.N., Simulation of indoor temperature and humidity conditions including hygrothermal interactions with building envelope Solar Energy 78 (2005) 554–561.
-
[Mendes2019] Mendes, N., Chhay, M., Berger, J. and Dutykh, D., Numerical methods for diffusion phenomena in building physics, Springer Nature Switzerland AG 2019.
-
[Neymark2002] Neymark, J. and Judkoff, R. International energy agency building simulation test and diagnostic method for heating, ventilation, and air-conditioning equioement models (HVAC BESTEST). Volume 1: Cases E100-E200 Technical Report NREL/TP-550-30152.
-
[Škerget2014] Škerget, L. and Tadeu, A. BEM numerical simulation of coupled heat and moisture flow through a porous solid Engineering Analysis with Boundary Elements, 2014.
-
[Straube2002] Straube J. F., Moisture in Buildings, ASHRAE Jornal, January 2002.