View Factor

To compute radiation exchange between any two surfaces, the concept of a view factor must be introducced, see [Modest].

View factor is also called configuration or shape factor.

1. General expression

The view factor \(F_{A_i \rightarrow A_j}\) is defined as the fraction of the radiation leaving surface i that is intercepted by surface j. To develop a general expression for \(F_{A_i \rightarrow A_j},\) we consider the arbitrarily oriented surfaces \(A_{i}\) and \(A_j\). Elemental areas on each surface, \(d A_{i}\) and \(d A_j\) are connected by a line of length \(R\), which forms the polar angles \(\theta_{i}\) and \(\theta_j,\) respectively, with the surface normals \(\mathbf{n}_{i}\) and \(\mathbf{n}_j\). \(I_{e+r,i}\) is the intensity of radiation leaving surface \(i\) by emission and reflection. The values of \(R, \theta_{i},\), \(\theta_j\) and \(I_{e+r,i}\) vary with the position of the elemental areas on \(A_{i}\) and \(A_j\)

Figure 1. View Factor of any two surfaces

\[F_{A_i \rightarrow A_j} = \frac{\int_{A_i}{ \int_{A_j}{I_{r+e,i} \frac{cos \theta_i cos \theta_j}{R^2} dA_j} dA_i}}{\pi \int_{A_i}{ I_{r+e,i} dA_i }}\]

In the other hand :

\[F_{A_i \rightarrow A_j} = \frac{\int_{A_j}{ \int_{A_i}{ I_{r+e,j} \frac{cos \theta_j cos \theta_i}{R^2} dA_i} dA_j}}{\pi \int_{A_j}{ I_{r+e,j} dA_j }}\]

1.1. Details

We introduce \(dF_{dA_i \rightarrow dA_j}\) the view factor between the infinitesimal \(dA_i\) and \(dA_j\).

From the definition of the radiation intensity, the rate at which radiation leaves \(d A_{i}\) and is intercepted by \(d A_j\) writes

\[d q_{dA_i \rightarrow dA_j} = I_{e+r, i} \cos \theta_{i} d A_{i} d \omega_{j-i}\]

where

\(d \omega_{j-i}\) is the solid angle associated to \(d A_j\) when viewed from \(d A_{i} .\)

We have that \(d \omega_{j-i} = \left(\cos \theta_j d A_j\right) / R^{2}\), we obtain

\[d q_{dA_i \rightarrow dA_j} = I_{e+r, i} \frac{\cos \theta_{i} \cos \theta_j}{R^{2}} d A_{i} d A_j\]

The total energy diffuse by the infinitesimal area \(dA_1\) is \(\pi I_{e+r, i}\).

The infinitesimal factor view write :

\[dF_{dA_i \rightarrow dA_j} = \frac{I_{e+r, i} \frac{\cos \theta_{i} \cos \theta_j}{R^{2}} d A_{i} d A_j}{\pi I_{e+r, i} dA_i}\]

\[dF_{dA_i \rightarrow dA_j} = \frac{cos \theta_i cos \theta_j}{\pi R^2} dA_j\]

The view factor between infinitesimal area and area (\(F_{dA_i \rightarrow A_j}\)). The total energy leaving \(dA_i\) toward all \(A_j\) is :

\[I_{e+r,i} dA_i \int_{A_j}{\frac{cos \theta_i \theta_j}{R^2}dA_j}\]

The view factor \(F_{dA_i \rightarrow A_j}\) between infinitesimal area and area writes :

\[F_{dA_i \rightarrow A_j} = \frac{I_{e+r,i} dA_i \int_{A_j}{\frac{cos \theta_i \theta_j}{\pi R^2}dA_j}}{\pi I_{e+r,i} dA_i}\]

\[F_{dA_i \rightarrow A_j} = \int_{A_j}{\frac{cos \theta_i \theta_j}{\pi R^2}dA_j}\]

The view factor between area and infinitesimal area (\(dF_{A_i \rightarrow dA_j}\)).

\[dF_{A_i \rightarrow dA_j} = \frac{\int_{A_j}{I_{e+r,i}\frac{cos \theta_i cos \theta_j}{R^2}dA_j dA_i}}{\pi \int_{A_j}{I_{e+r,i}}dA_j}\]

Finally, we see the view factor \(F_{A_i \rightarrow A_j}\) between two areas :

It remains to compute the total rate at which radiation leaves surface \(i\) and is intercepted by \(j\). We integrate over the two surfaces and get

\[q_{A_i \rightarrow A_j} = \int_{A_{i}} \int_{A_j} J_{i} \frac{\cos \theta_{i} \cos \theta_j}{R^{2}} d A_j d A_{i}\]

And the total diffuse energy :

\[q_{A_i \rightarrow tot} = \pi \int_{A_i}{I_{r+e,i}dA_i}\]

Thus, we have :

\[F_{A_i \rightarrow A_j} = \frac{q_{i \rightarrow i}}{q_{i \rightarrow tot}} = \frac{\int_{A_i}{ \int_{A_j}{I_{r+e,i} \frac{cos \theta_i cos \theta_j}{R^2} dA_j} dA_i}}{\pi \int_{A_i}{ I_{r+e,i} dA_i }}\]

2. Symplify expression

If the intensity of radiation leaving surface \(i\) (\(I_{e+r,i}\)) is independant of position, we can exit \(I_{e+r,i}\) under the integrals :

\[F_{A_i \rightarrow A_j} = \frac{1}{A_{i}} \int_{A_{i}} \int_{A_j} \frac{\cos \theta_{i} \cos \theta_j}{\pi R^{2}} d A_j d A_{i}\]

Similarly, if the intensity of radiation leaving surface \(j\) \(I_{e+r,j}\) is independant of position, we have :

\[F_{A_j \rightarrow A_i} = \frac{1}{A_j} \int_{A_j} \int_{A_{i}} \frac{\cos \theta_j \cos \theta_{i}}{\pi R^{2}} d A_{i} d A_j\]

These Equations can be used to compute the view factor associated with any two surfaces that are diffuse emitter and reflectors and have uniform radiosity.

If \(I_{e+r,i}\) is independant of position, the view factor between \(A_i\) and \(dA_j\) :

\[dF_{A_i \rightarrow dA_j} = \frac{1}{A_j} \int_{A_j}{\frac{cos \theta_i cos \theta_j}{\pi R^2}dA_j dA_i}\]

3. Relations

3.1. Reciprocity

From definition of infinitesiaml view factor and the simplify view factor, we have immediately the following relation, called the reciprocity relation:

Reciprocity relation between view factors

\(dA_{i} dF_{A_i \rightarrow A_j} = dA_j dF_{A_j \rightarrow A_i}\)
\(A_{i} F_{A_i \rightarrow dA_j} = dA_j F_{dA_j \rightarrow A_i}\) (if \(I_{e+r,i}\) is constant compared the position)
\(A_{i} F_{A_i \rightarrow A_j}=A_j F_{A_j \rightarrow A_i}\) (if \(I_{e+r,i}\) and \(I_{e+r,j}\) are constant compared the position)

this necessary relation can be used to verify computations of view factors.

3.2. Summation rule in enclosure

If we placed in case of view factor simplify. When considering surfaces of an enclosure, the summation rule applies to each of the \(N\) surfaces in the enclosure

\[\sum_{j=1}^{N} F_{A_i \rightarrow A_j}=1.\]

This rule follows from the conservation requirement that all radiation leaving surface \(i\) must be intercepted by the enclosure surfaces.

The term \(F_{A_i \rightarrow A_i}\)

The term \(F_{A_i \rightarrow A_i}\) appearing in this summation represents the fraction of the radiation that leaves surface \(i\) and is directly intercepted by \(i\):

If the surface is concave, it sees itself and \(F_{A_i \rightarrow A_i}\) is nonzero.
However, for a plane or convex surface, \(F_{A_i \rightarrow A_i}=0\)

3.3. Subsurface Summation

3.3.1. Summation by \(A_j\)

If we placed in case of view factor simplify. If the area \(A_j\) can be decompose by different sub-areas : \(A_j = \bigcup_{l=1}^{L}{A_{(j,l)}}\) :

\[F_{A_i \rightarrow A_j} = \sum_{l=1}^{L}{F_{A_i \rightarrow A_{(j,l)}}}\]

3.3.2. Summation by \(A_i\)

If we placed in case of view factor simplify. If the area \(A_i\) can be decompose by different sub-areas : \(A_i = \bigcup_{k=1}^{K}{A_{(i,k)}}\), to use summation by \(A_j\) and reciprocity rule :

\[F_{A_i \rightarrow A_j} = \frac{1}{A_i} \sum_{k=1}^{K}{ A_{(i,k)} F_{A_{(i,k)} \rightarrow A_j}}\]

Remarks : It’s weighted average by areas.

3.3.3. Summation by \(A_i\) and \(A_j\)

If we placed in case of view factor simplify. If the area \(A_i\) and \(A_j\) can be decompose by different sub-areas : \(A_i = \bigcup_{k=1}^{K}{A_{(i,k)}}\) and \(A_j = \bigcup_{l=1}^{L}{A_{(j,k)}}\) , to combine summation by \(A_j\)and summation by \(A_i\) :

\[F_{A_i \rightarrow A_j} = \frac{1}{A_i} \sum_{k=1}^{K}{ \left( A_{(i,l)} \sum_{l=1}^{L}{F_{A_{(i,k)} \rightarrow A_{(j,l)}}} \right) }\]

4. Few example of factor view

4.1. Angle of two walls

The view factor between two walls wich form a right angle :

Figure 2. Angle of two walls

\[\begin{eqnarray} F_{A_1 \rightarrow A_2} = & \frac{1}{\pi W} \left( W tan^{-1} \left( \frac{1}{W} \right) + H tan^{-1} \left( \frac{1}{H} \right) - \sqrt{H^2+W^2} tan^{-1} \left( \frac{1}{\sqrt{H^2+W^2}} \right) \right. \\ &+ \left. \frac{1}{4} ln \left( \frac{(1+W^2)(1+H^2)}{1+W^2+H^2} \left( \frac{W^2(1+W^2+H^2)}{(1+W^2)(W^2+H^2)} \right)^{W^2} \left( \frac{H^2(1+H^2+W^2)}{(1+H^2)(H^2+W^2)} \right)^{H^2} \right) \right) \end{eqnarray}\]

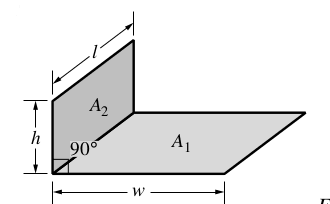
With :

\(H=\frac{h}{l}\)
\(W=\frac{w}{l}\)

4.2. Two parallel walls

The view factor between two parallel walls :

Figure 3. Parallel walls

\[F_{A_1 \rightarrow A_2} = \frac{2}{\pi X Y} \left( ln \left( \frac{(1+X^2)(1+Y^2)}{1+X^2+Y^2} \right)^{1/2} + X \sqrt{1+Y^2} tan^{-1} \left( \frac{X}{\sqrt{1+Y^2}} \right) + Y \sqrt{1+X^2} tan^{-1} \left( \frac{Y}{\sqrt{1+X^2}} \right) - X tan^{-1}(X) - Y tan^{-1}(Y) \right)\]

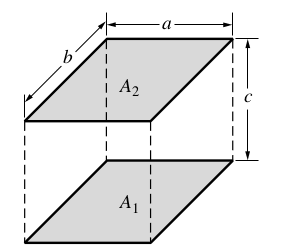
With :

\(X=\frac{a}{c}\)
\(Y=\frac{b}{c}\)

References

[Incropera] Fundamentals of Heat and Mass Transfer, Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, David P. DeWitt, Wiley.
[Kumaran1996] Kumaran, M. Kumar, Heat, Air and Moisture Transfer in Insulated Envelope Parts, Final Report, Volume 3.
[Ozturk] Abdurrahman Ozturk, Implementation of View Factor Model and Radiative Heat Transfer Model in MOOSE. University of South Carolina, Download PDF
[Modest] M.F. Modest, Radiative Heat Transfet. Elsevier Science, 2013, ISBN 9780123869906, Chapter 8
[Visionary] Visionaray: A Cross-Platform Ray Tracing Template Library, Zellmann, Stefan and Wickeroth, Daniel and Lang, Ulrich, Proceedings of the 10th Workshop on Software Engineering and Architectures for Realtime Interactive Systems (IEEE SEARIS 2017), 2017
[Visionary::github] Visionaray, Zellman, github.com/szellmann/visionaray