Geometry’s Tools

This page details the tools of geometry useful for Monte Carlo method.

1. In surface ?

In this section, we detail how an point of plan is in geometrical object (square, traingle) of this plan.

1.1. Point in triangle

Set a triangle $\mathcal{T}$ (origin point $P$, directional vector $\mathbf{e_1}$ and $\mathbf{e_2}$) and point $Q$ in plan of the square.

\[Q \in \mathcal{T} \Longleftrightarrow \left\{ \begin{eqnarray} 0 \leq u \leq 1 \\ 0 \leq v \leq 1 \\ u + v \leq 1 \end{eqnarray} \right.\]

With :

\[\begin{eqnarray} u &=& \frac{(\mathbf{e_2} \cdot \mathbf{e_2}) (\vec{PQ} \cdot \mathbf{e_1}) - (\mathbf{e_1} \cdot \mathbf{e_2}) (\vec{PQ} \cdot \mathbf{e_2}) }{(\mathbf{e_1} \cdot \mathbf{e_1})(\mathbf{e_2} \cdot \mathbf{e_2})-(\mathbf{e_1} \cdot \mathbf{e_2})^2} \\ v &=& \frac{(\mathbf{e_1} \cdot \mathbf{e_1}) (\vec{PQ} \cdot \mathbf{e_2}) - (\mathbf{e_1} \cdot \mathbf{e_2}) (\vec{PQ} \cdot \mathbf{e_1}) }{(\mathbf{e_1} \cdot \mathbf{e_1})(\mathbf{e_2} \cdot \mathbf{e_2})-(\mathbf{e_1} \cdot \mathbf{e_2})^2} \end{eqnarray}\]

Proof :

\[\begin{eqnarray} Q = P + u \mathbf{e_1} + v \mathbf{e_2} \\ \vec{PQ} = u \mathbf{e_1} + v \mathbf{e_2} \end{eqnarray}\]

We have :

\[\begin{eqnarray} \vec{PQ} \cdot \mathbf{e_1} &=& \left( u \mathbf{e_1} + v \mathbf{e_2} \right) \cdot \mathbf{e_1} \\ &=& u \mathbf{e_1} \cdot \mathbf{e_1} + v \mathbf{e_1} \cdot \mathbf{e_2} \end{eqnarray}\]

And :

\[\begin{eqnarray} \vec{PQ} \cdot \mathbf{e_2} &=& \left( u \mathbf{e_1} + v \mathbf{e_2} \right) \cdot \mathbf{e_2} \\ &=& u \mathbf{e_2} \cdot \mathbf{e_2} + v \mathbf{e_1} \cdot \mathbf{e_2} \end{eqnarray}\]

We have an linear equation with two unknowns :

And to have $Q$ is in $\mathcal{T}$, we have the condition :

\[\left\{ \begin{eqnarray} 0 \leq u \leq 1 \\ 0 \leq v \leq 1 \\ u + v \leq 1 \end{eqnarray} \right.\]

1.2. Point in square

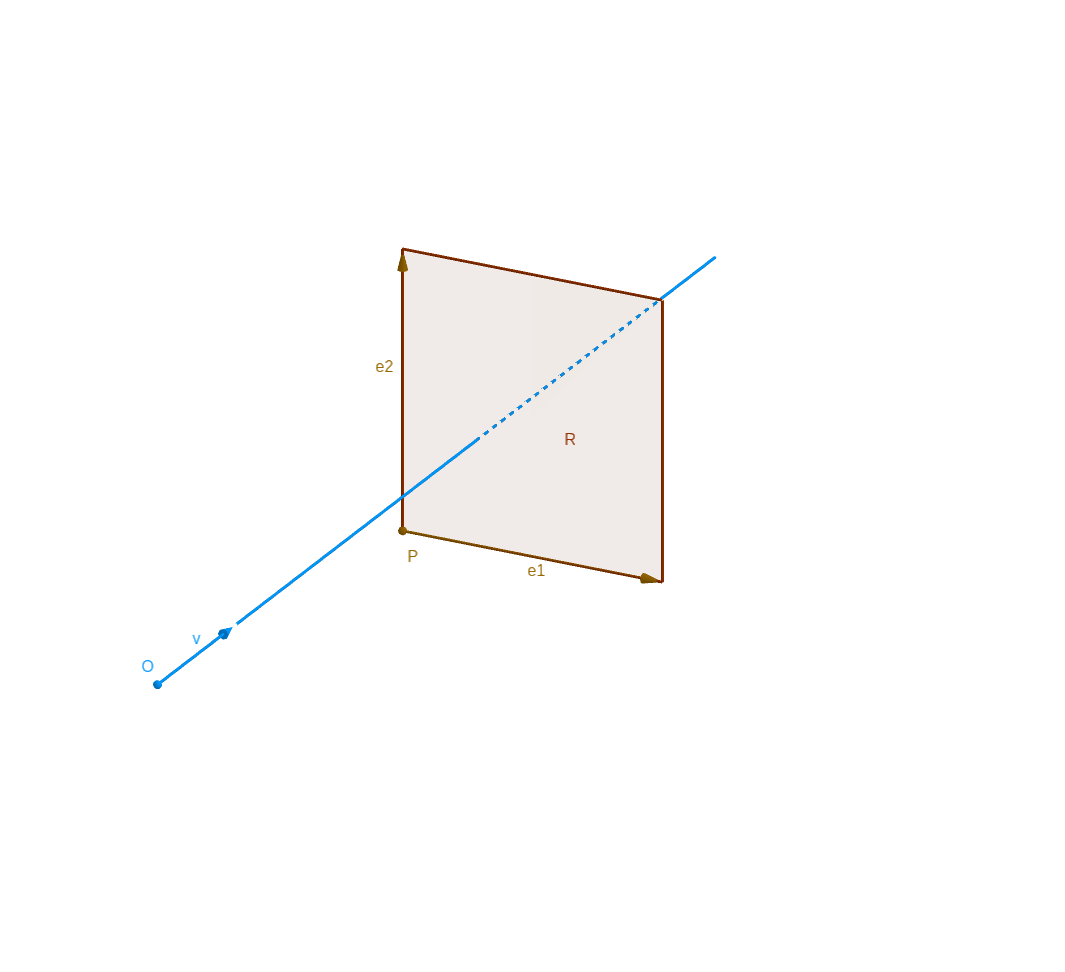
Set a square $\mathcal{R}$ (origin point $P$, directional vector $\mathbf{e_1}$ and $\mathbf{e_2}$) and point $Q$ in plan of the square.

\[Q \in \mathcal{R} \Longleftrightarrow \left\{ \begin{eqnarray} 0 \leq \frac{\vec{QP} \cdot \mathbf{e_1}}{||\mathbf{e_1}||^2} \leq 1 \\ 0 \leq \frac{\vec{QP} \cdot \mathbf{e_2}}{||\mathbf{e_2}||^2} \leq 1 \end{eqnarray} \right.\]

Remark : we can simplifiate the formula to remplace $||\mathbf{e_1}||$ and $||\mathbf{e_2}||$ by the side of $\mathcal{R}$.

Proof :

\[\begin{eqnarray} Q = P + u \mathbf{e_1} + v \mathbf{e_2} \\ \vec{QP} = u \mathbf{e_1} + v \mathbf{e_2} \\ \vec{QP} \cdot \mathbf{e_1} = u \mathbf{e_1} \cdot \mathbf{e_1} + 0 \\ u = \frac{\vec{QP} \cdot \mathbf{e_1}}{||\mathbf{e_1}||^2} \end{eqnarray}\]

And we must have the condition : $0 \leq u \leq 1$ if we want to have $Q$ in square $\mathcal{R}$.

It the same for $v$.

2. Method of Visionaray

This section retake the geometrical method of visionaray.

2.1. Interception by segment

The question is : When the right $\mathcal{C}$ (of origin $O$ and of direction $\mathbf{v}$) intersect the segment $\mathcal{Q}$ (of vertex $A$ and $B$) ?

Figure 1. Intersection of ray and segment

We detail the coordonna :

$A = \begin{pmatrix} x_A \\ y_A \\ z_A \end{pmatrix}$
$B = \begin{pmatrix} x_B \\ y_B \\ z_B \end{pmatrix}$
$\mathbf{v} = \begin{pmatrix} x_v \\ y_v \\ z_v \end{pmatrix}$

We introduce :

$t_1 = \frac{\vec{OA}}{\mathbf{v}}$ (term to term division)
$t_2 = \frac{\vec{OB}}{\mathbf{v}}$

\[\begin{eqnarray} t_{near} &= max \left( min \left( x_{t_1}, x_{t_2} \right), min \left( y_{t_1}, y_{t_2} \right), min \left( z_{t_1}, z_{t_2} \right) \right) \\ t_{far} &= min \left( max \left( x_{t_1}, x_{t_2} \right), max \left( y_{t_1}, y_{t_2} \right), max \left( z_{t_1}, z_{t_2} \right) \right) \end{eqnarray}\]

\[\mathcal{C} \text{ intersect } \mathcal{Q} \Longleftrightarrow t_{near} \leq t_{far}\]

2.2. Interception by triangle

The question is : When the right $\mathcal{C}$ (of origin $O$ and of direction $\mathbf{v}$) intersect the triangle $\mathcal{T}$ (of origin $P$ and of vector $\mathbf{e_1}, \mathbf{e_2}$) ? (we suppose to $O \notin$ plan of $\mathcal{T}$)

Figure 2. Intersection of ray and triangle

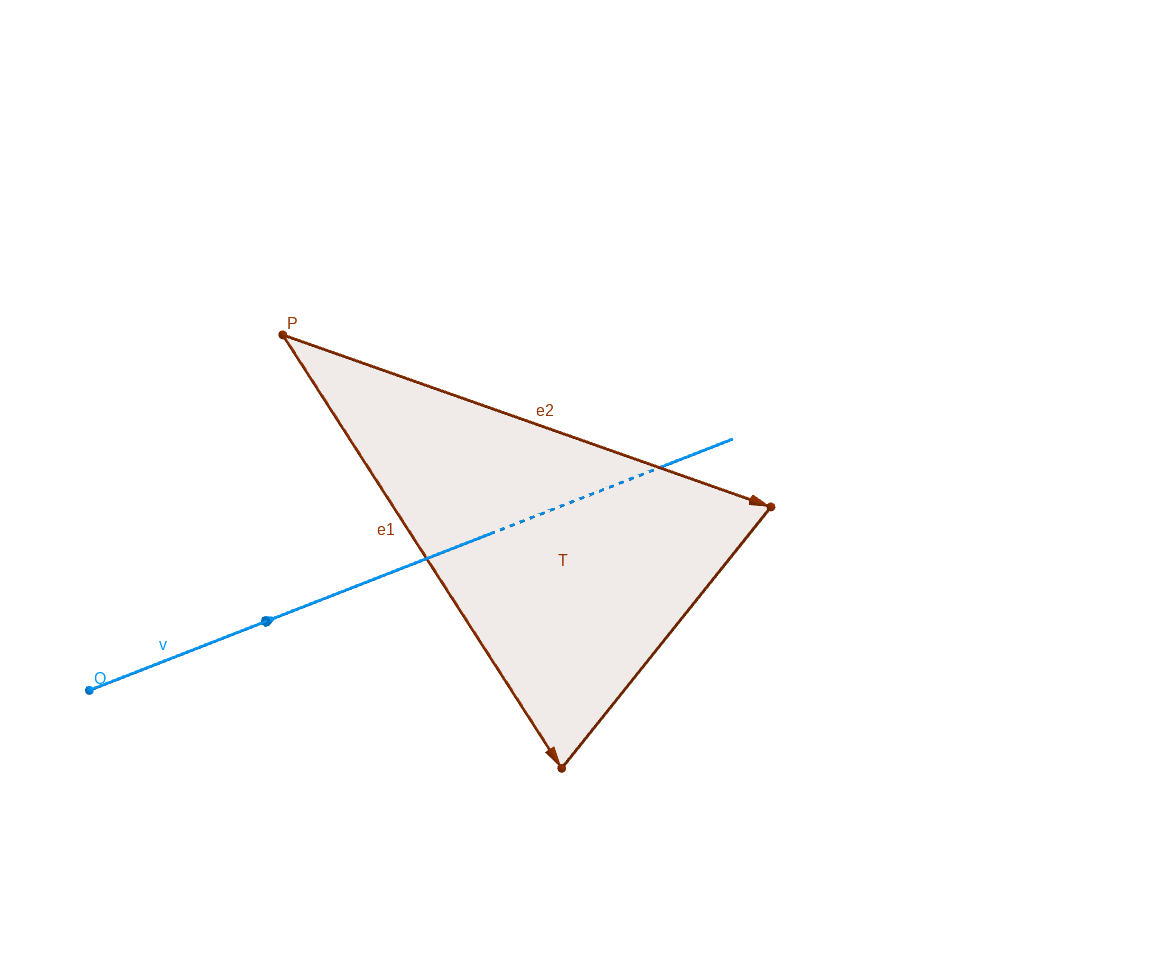
First, we verify if $\mathbf{v}$ is parallel of plan of triangle $\mathcal{T}$ (obviously, if it case, the prolonged right of $\mathcal{C}$ doesn’t intersect $\mathcal{T}$) :

\[\left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} = 0 \Leftrightarrow \text{ $\mathbf{v}$ is parallel of plan of triangle $\mathcal{T}$ }\]

Or, the contraposed :

\[\left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} \ne 0 \Leftrightarrow \text{ intersection of prolonged right of } \mathcal{C} \text{ and plan of } \mathcal{T} \text{ exists }\]

Remark : $\left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} = \left( \mathbf{v} \wedge \mathbf{e_1} \right) \cdot \mathbf{e_2} $

We want $\left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} \ne 0$.

Proof : With the rule of calculation of scalar and vectorial produce, we have :

\[\left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} = \mathbf{v} \cdot \left( \mathbf{e_2} \wedge \mathbf{e_1} \right)\]

And : $\mathbf{e_2} \wedge \mathbf{e_1}$ is a normal vector of plan of the triangle $\mathcal{T}$.

Thus :

\[\begin{eqnarray} \mathbf{v} \cdot \left( \mathbf{e_2} \wedge \mathbf{e_1} \right) = 0 &\Longleftrightarrow \mathbf{v} \text{ is orthogonal to } \mathbf{e_2} \wedge \mathbf{e_1} \\ &\Longleftrightarrow \mathbf{v} \text{ is parallel to plan of } \mathcal{T} \end{eqnarray}\]

After we consider to $\mathbf{v} \cdot \left( \mathbf{e_2} \wedge \mathbf{e_1} \right) \ne 0$.

Second, we verify if the intersection is in triangle $\mathcal{T}$

\[\begin{eqnarray} 0 \leq \frac{\vec{PO} \cdot (\mathbf{v} \wedge \mathbf{e_2})}{ (\mathbf{v} \wedge \mathbf{e_2}) \cdot \mathbf{e_1} } \leq 1 \\ 0 \leq \frac{\vec{PO} \cdot (\mathbf{v} \wedge \mathbf{e_1})}{ (\mathbf{v} \wedge \mathbf{e_1}) \cdot \mathbf{e_2} } \leq 1 \end{eqnarray}\]

Proof : We exprim the space :

\[\begin{eqnarray} &\mathcal{T} = \{ t \mathbf{e_1} + u \mathbf{e_2} + P \in \mathbb{R}^3, 0 \leq t,u \leq 1, u+t \leq 1 \} \\ &\mathcal{C} = \{ O + \lambda \mathbf{v} \in \mathbb{R}^3, \lambda \in \mathbb{R} \} \end{eqnarray}\]

The intersection is :

\[\begin{eqnarray} &Q = \mathcal{T} \cap \mathcal{C} \\ &Q = t \mathbf{e_1} + u \mathbf{e_2} + P = O + \lambda \mathbf{v} \text{ with } 0 \leq t,u \leq 1, u+t \leq 1 \text{ and } \lambda \in \mathbb{R} \end{eqnarray}\]

We want to manipulate the equation :

\[t \mathbf{e_1} + u \mathbf{e_2} + \vec{OP} = \lambda \mathbf{v}\]

\[\begin{eqnarray} \left( t \mathbf{e_1} + u \mathbf{e_2} + \vec{OP} \right) \wedge \mathbf{v} &= \lambda \mathbf{v} \wedge \mathbf{v} = 0 \\ \left( \left( t \mathbf{e_1} + u \mathbf{e_2} + \vec{OP} \right) \wedge \mathbf{v} \right) \cdot \mathbf{e_1} &= 0 \\ \left( t \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} + \left( u \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} + \left( \vec{OP} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} &= 0 \\ t \left( \mathbf{e_1} \wedge \mathbf{e_1} \right) \cdot \mathbf{v} + \left( u \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} + \left( \vec{OP} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} &= 0 \\ 0 + \left( u \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} + \left( \vec{OP} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} &= 0 \\ u = - \frac{\left( \vec{OP} \wedge \mathbf{v} \right) \cdot \mathbf{e_1}}{\left( \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1}} \\ u = \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \end{eqnarray}\]

In the same way :

\[t = \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} }\]

Thus, we have the condition :

\[\left\{ \begin{eqnarray} 0 \leq t &= \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} } \leq 1 \\ 0 \leq u &= \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \leq 1 \\ t+u &= \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } + \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \leq 1 \end{eqnarray} \right.\]

Recapitulation :

\[\text{The ray } \mathcal{C} \text{ is intersept by } \mathcal{T} \Longleftrightarrow \left\{ \begin{eqnarray} \left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} \ne 0 \\ 0 \leq \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} } \leq 1 \\ 0 \leq \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \leq 1 \\ \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } + \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \leq 1 \end{eqnarray} \right.\]

2.3. Interception by parallelogram

We can adapt the recapitulation to have the intersction between right and parallelogram $\mathcal{R}$ (of origin point $P$ and directional vector $\mathbf{e_1}$ and $\mathbf{e_2}$)

Figure 3. Intersection of ray and square

\[\text{The ray } \mathcal{C} \text{ is intersept by } \mathcal{R} \Longleftrightarrow \left\{ \begin{eqnarray} \left( \mathbf{v} \wedge \mathbf{e_2} \right) \cdot \mathbf{e_1} \ne 0 \\ 0 \leq \frac{ \vec{OP} \cdot \left( \mathbf{e_2} \wedge \mathbf{v} \right)}{\left( \mathbf{e_2} \wedge \mathbf{v} \right) \cdot \mathbf{e_1} } \leq 1 \\ 0 \leq \frac{ \vec{OP} \cdot \left( \mathbf{e_1} \wedge \mathbf{v} \right)}{\left( \mathbf{e_1} \wedge \mathbf{v} \right) \cdot \mathbf{e_2} } \leq 1 \end{eqnarray} \right.\]

2.4. Interception by plan

\[\text{ the semi-right $\mathcal{C}$ (of origin $O$ and direction $\mathbf{v}$) intersect the plan $\mathcal{P}$ (of normal $\mathbf{n}$) } \Longleftrightarrow \mathbf{v} \wedge \mathbf{n} \ne 0\]

Figure 4. Intersection of ray and plan

Proof : We have

\[\begin{eqnarray} \mathcal{C} \text{ intersect } \mathcal{P} &\Longleftrightarrow& \mathbf{v} \text{ not parallel to } \mathbf{n} \\ &\Longleftrightarrow& \mathbf{v} \wedge \mathbf{n} \ne 0 \end{eqnarray}\]

3. Visibility between two plan

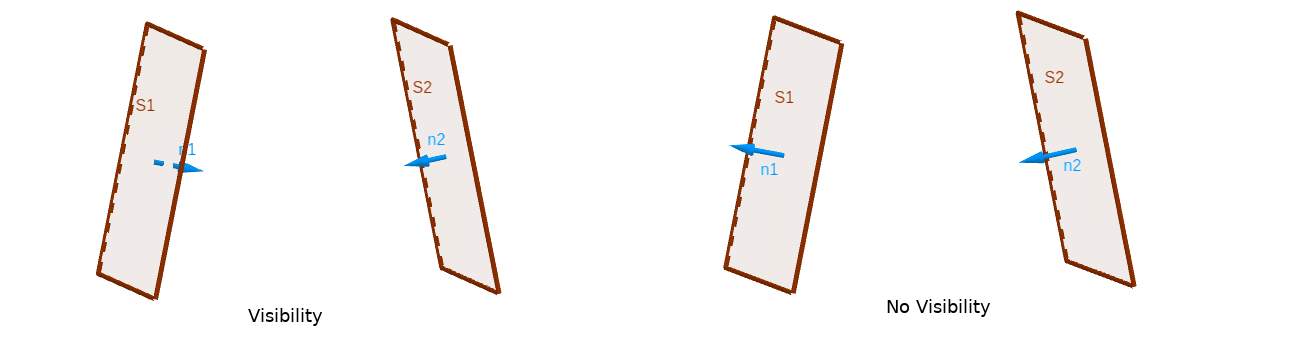
Before to calculate the view factor between two surface, we must know if they visible from each one

We must define a oriented surface, what side is emit and absorp of surface.

Example 1. Definition of oriented surface

A oriented surface is a surface (suppose contain in plan), is a surface with an oriented normal.

Set oriented surfaces $S_1$ and $S_2$ (with oriented normal : $\mathbf{n_1}$ and $\mathbf{n_2}$) :

\[S_1 \text{ and } S_2 \text{ are visible } \Longleftrightarrow \mathbf{n_1} \cdot \mathbf{n_2} < 0\]

Figure 5. Visibility between two surface

4. Convertion cartesian/polar

5. Detail of Triangle

Thus a triangle $\mathcal{T}$ of origin point $P$ and directional vector $\mathbf{e_1}$ and $\mathbf{e_2}$.

The center of $\mathcal{T}$ is $C = P + \frac{1}{3} \mathbf{e_1} + \frac{1}{3} \mathbf{e_2}$ and the ray of circumscribed circle $R = ||\vec{CP}|| = \frac{1}{3} || \mathbf{e_1} + \mathbf{e_2}||$