Benchmarks

1. Introduction

This section details the benchmarks of calculation of view factor. To see the formula see View Factor

Two examples are use :

  • walls which form an right angle

  • parallele walls

The during of code is measure and the result is compared with the theorical exact value (see…​).

2. Angle of Walls

2.1. Presentation

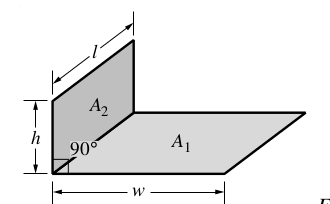
wall angle
Figure 1. Geometrie of angle of wall

The geometry of this benchmarks is two walls wich form an right angle with dimension :

  • length w = 1

  • height h = 1

  • depth l = 1

To see the formula of view factor between two walls in angle

gmsh wall angle
Figure 2. gmsh of geometrie

2.2. Execution

To execute angle_walls.cpp :

  • Compile with *g* : g angle_walls.cp -o angle_walls

  • Execute : ./angle_walls N_s N_r (N_s is the number of source point generated and N_r the number of emissive ray generated by one source)

2.3. Results

The results are (with \(N_s=1000\), \(N_r=1000\)) :

  • theorical value : \(0.222937\)

  • monte carlo method value : \(0.089387\)

The during of method is \(17356572 ms\)

PROBLEM : the result with monte carlo method isn’t the expected result.

3. Parallel Walls

3.1. Presentation

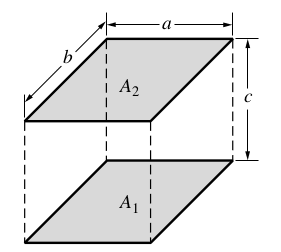
wall parallel
Figure 3. Geometrie of parallel wall

The geometry of this benchmarks is two parallel walls with dimension :

  • length a = 1

  • width b = 1

  • height c = 1

To see the formula of view factor between two parallel walls.

gmsh wall parallel
Figure 4. Geometrie of parallel wall

3.2. Execution

To execute parallel_walls.cpp :

  • Compile with *g* : g parallel_walls.cp -o parallel_walls

  • Execute : ./parallel_walls N_s N_r (N_s is the number of source point generated and N_r the number of emissive ray generated by one source)

3.3. Results

The results are (with \(N_s=1000\), \(N_r=1000\)) :

  • theorical value : \(0.199825\)

  • monte carlo method value : \(0.131721\)

The during of method is \(282236 ms\)

PROBLEM : the result with monte carlo method isn’t the expected result.