MonteCarlo
1. Introduction
The goal of MonteCarlo method is to calculate the heat transfert between two surface. MonteCarlo method use finite element and probabilist theory.
First, the MonteCarlo method calculates the view factor between two surface.
The MonteCarlo method consist to decompose the surfaces (emissive surface \(A_i\) and absortive surface \(A_j\)) in little finite element. Here the finite element is triangle.
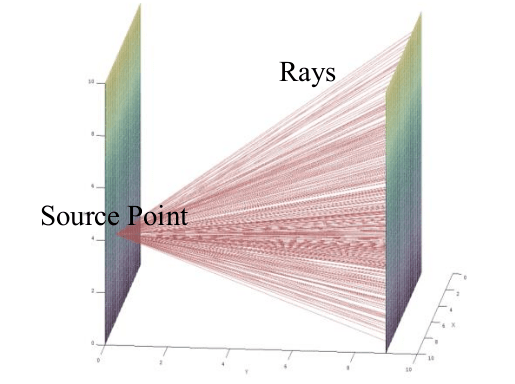
We generate \(N_r\) random ray from \(N_s\) random source point, from emissive surface \(A_i\). Those rays touch the finite element of absorbent surface \(A_j\).
The local view factor between element \(e^i_k\) of \(A_i\) and element \(e^j_l\) of \(A_j\) is calculate by subsurface summation :
With :
-
\(N=N_s N_r\) the total number of rays generate by \(A_i\)
-
\(n\) the number of rays generate by \(A_i\) intercept by \(A_j\)
After calculating all local view factor, we can compute the global view factor with :
After calculating the view factor, it calculates the heat transfert between surfaces \(A_i\) and \(A_j\), with the formula :
With \(T_i\) the absolute temperature of \(A_i\) and \(T_j\) the absolute temperature of \(A_j\).
2. Tools
2.1. Visibility of surface
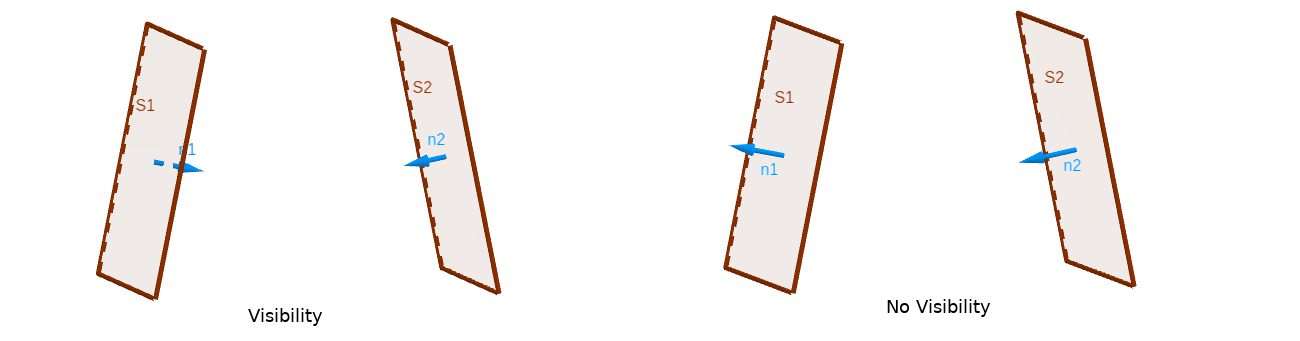
Before calculating the view factor, it is interesting to know if the to surface are visible to each other.
For that, we use the oriented normal associated to element.
Set oriented surfaces element \(S_1\) and \(S_2\) (with oriented normal : \(\mathbf{n_1}\) and \(\mathbf{n_2}\)) :
2.2. Distribution of random ray
For the emissive element, we generate some \(N_s\) source point and \(N_r\) ray from one source point.
For that we choose good supposition on matters :
-
homogeneous (the emission is the same for any position)
-
anisotropic (the emission is the same for any direction)
The distributions :
-
Source point \(O\) : \(\left\{\begin{eqnarray} x_O = x_C + R \sqrt{\xi_2} cos(2\pi \xi_1) \\ y_O = x_C + R \sqrt{\xi_2} sin(2\pi \xi_1) \end{eqnarray}\right.\) with \(\xi_1\) and \(\xi_2\) wich follow uniformely distribution in \([0,1]\) until in finite element.
-
Incident angle \(\phi\) of ray follow uniformely distribution in \([0,2\pi]\)
-
Azimuthal angle \(\theta\) of ray follow uniformely distribution in \([0,\pi]\)
For more detail, see the section Distribution of random rays.
2.3. Interception of ray by square
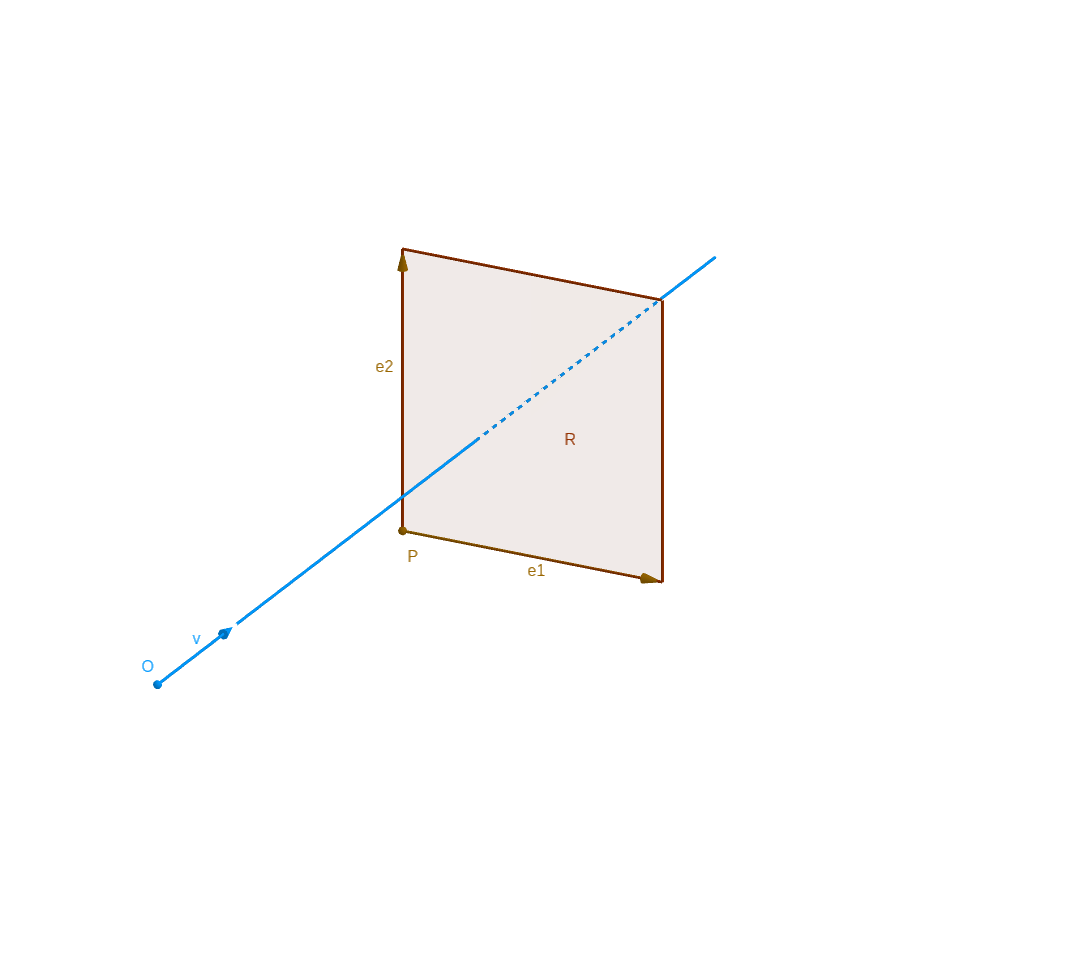
We have the conditon to intersection between right and square \(\mathcal{R}\) (of origin point \(P\) and directional vector \(\mathbf{e_1}\) and \(\mathbf{e_2}\)).
References
-
[Incropera] Fundamentals of Heat and Mass Transfer, Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera, David P. DeWitt, Wiley.
-
[Kumaran1996] Kumaran, M. Kumar, Heat, Air and Moisture Transfer in Insulated Envelope Parts, Final Report, Volume 3.
-
[Ozturk] Abdurrahman Ozturk, Implementation of View Factor Model and Radiative Heat Transfer Model in MOOSE. University of South Carolina, Download PDF
-
[Modest] M.F. Modest, Radiative Heat Transfet. Elsevier Science, 2013, ISBN 9780123869906, Chapter 8
-
[Visionary] Visionaray: A Cross-Platform Ray Tracing Template Library, Zellmann, Stefan and Wickeroth, Daniel and Lang, Ulrich, Proceedings of the 10th Workshop on Software Engineering and Architectures for Realtime Interactive Systems (IEEE SEARIS 2017), 2017
-
[Visionary::github] Visionaray, Zellman, github.com/szellmann/visionaray