Modeling and Simulation of Radiative Heat Transfer

Heat transfer by conduction and convection requires the presence of a temperature gradient in some form of matter. However heat transfer by thermal radiation requires no matter. It is an important process relevant to many industrial heating, cooling, and drying processes, as well as to energy conversion methods that involve for example solar radiation.

We shall consider

radiation processes and associated properties
radiation between surfaces

A glossary summarizes the many terms involved in radiative heat transfer.

1. Simple Definition

Radiative heat transfer could be defined in a very simplified statement as the interchange of electromagnetic waves between surfaces of differing temperatures which can see each other. The full definition is however extensive and complex.

All surfaces which are above absolute zero \(\left(-273.15^{\circ} \mathrm{C} \text { or } 0.0 \mathrm{K}\right)\) are emitting radiant heat or absorbing, reflecting and transmitting heat radiation depending upon

whether they are emitting surfaces or receiving surfaces
and upon whether the material is opaque or transparent.

The distinction between an emitting surface and a receiving surface is dependent upon its temperature in relation to other surfaces it can 'see'.

1.1. Surface phenomenon

Radiation can be considered as surface phenomenon.

2. Fundamental concepts

Radiation originates due to emission by matter and that its subsequent transport does not require the presence of any matter. One theory views radiation as the propagation of a collection of particles termed photons or quanta. Another considers radiation as the propagation of electro-magnetic waves.

In both case, we associate radiation the standard wave properties of frequency \(v\) and wavelength \(\lambda\).

For radiation propagating in a particular medium, the two properties are related by

\[\lambda=\frac{c}{v}\]

where \(c\) is the speed of light in the medium. For propagation in a vacuum, \(c_{o}=\) \(2.998 \times 10^{8} \mathrm{m} / \mathrm{s} .\) The unit of wavelength is commonly the micrometer \((\mu \mathrm{m}),\) where \(1 \mu \mathrm{m}=10^{-6} \mathrm{m}\).

The portion of the electromagnetic spectrum of interest for radiation extends from approximately 0.1 to \(100 \mu \mathrm{m}\). It includes a portion of the UV and all of the visible and infrared (IR). It is defined as thermal radiation because it is both caused by and affects the thermal state or temperature of matter. It is why thermal radiation is pertinent to heat transfer.

Some definitions:

Spectral: refers to the dependence of the radiation magnitude with respect to the wavelength. The spectral distribution varies with the nature and the temperature of the emitting of the surface.
Directionality: a surface may emit in preferred directions generating a directional distribution of the emitted radiation.

spectral and directional effects of thermal radiation must be both considered to understand the concepts of emission, absorption, reflection, and transmission.

3. Radiation fluxes

Several radiation fluxes can be defined.a

Emissive power, \(E\left(\mathrm{W} / \mathrm{m}^{2}\right)\): the rate at which radiation is emitted from a surface per unit surface area, over all wavelengths and in all directions. This emissive power is associated to the behavior of a blackbody through the relation \(\left.E=\varepsilon \sigma T_{s}^{4} \right),\) where \(\varepsilon\) is a surface property known as the emissivity.

Radiation may consist of multiple surfaces at various temperatures. It is is incident upon the surface. The surface may also be irradiated by the sun.

Irradiation, \(G\left(\mathrm{W} / \mathrm{m}^{2}\right),\): rate at which radiation is incident upon the surface per unit surface area, over all wavelengths and from all directions

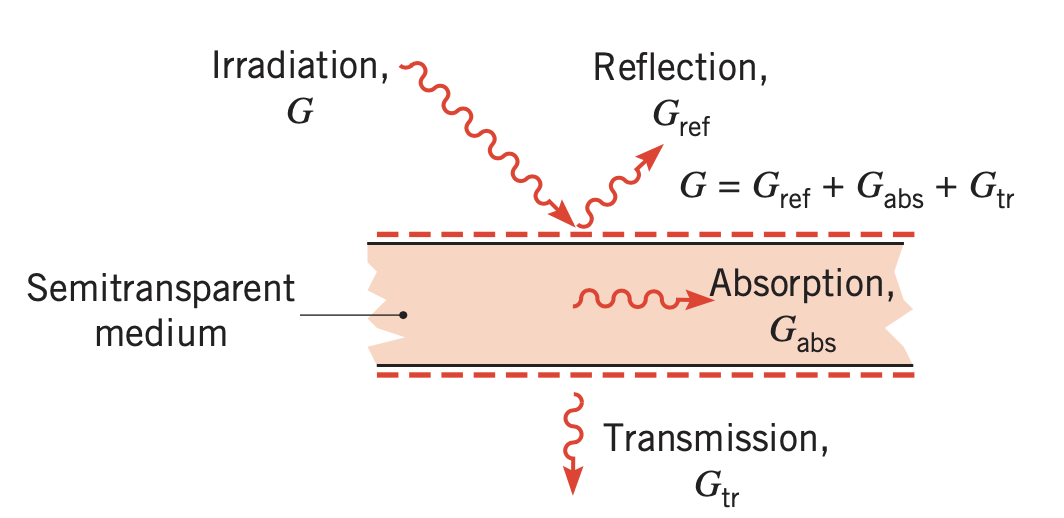
We now consider two types of medium: (i) semitransparent medium and (ii) opaque medium to understand what happens to radiation when it reaches a surface see below.

Irradiation reaching a semitransparent may be reflected, absorbed, and transmitted.

Transmission: radiation passing through the medium, as occurs when a layer of water or a glass plate is irradiated by the sun or artificial lighting. Denote the transmissivity \(\tau\), the fraction of the irradiation that is transmitted.
Absorption: radiation interacting with the medium, causing an increase in the internal thermal energy of the medium. Denote absorptivity \(\alpha\) as the fraction of the irradiation that is absorbed.
Reflection: radiation being redirected from the surface, with no effect on the medium. Denote reflectivity \(\rho\) as the fraction of the irradiation that is reflected.

We have that

\[\rho+\alpha+\tau=1\]

In case of opaque medium, there is no transmission (i.e \(\tau = 0\)), we have then

\[ \rho+\alpha=1\]

The last two fluxes can now be defined :

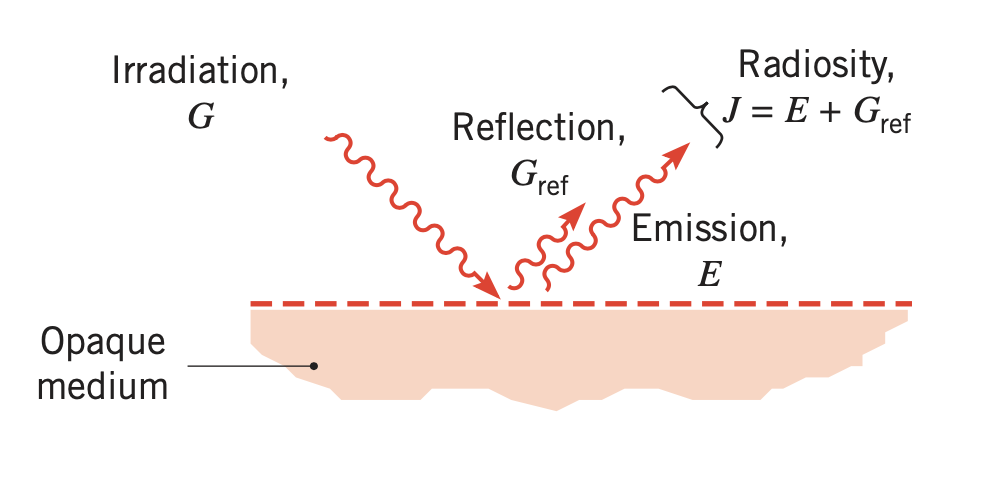
Radiosity, \(J\left(\mathrm{W} / \mathrm{m}^{2}\right)\): accounts for all the radiant energy leaving a surface.

For an opaque surface, it includes emission and the reflected portion of the irradiation. We have

\[J=E+G_{\mathrm{ref}}=E+\rho G\]

Radiosity can also be defined at a surface of a semitransparent medium. In that case, the radiosity leaving the top surface would include radiation transmitted through the medium from below.

Net radiative flux, \(q_{\mathrm{rad}}^{\prime \prime}\left(\mathrm{W} / \mathrm{m}^{2}\right),\): difference between the outgoing and incoming radiation

\[q_{\mathrm{rad}}^{\prime \prime}=J-G\]

For an opaque medium, we have

\[q_{\mathrm{rad}}^{\prime \prime}=E+\rho G-G=\varepsilon \sigma T_{s}^{4}-\alpha G\]

For a semitransparent surface including transmissivity as well, we have a similar formula.

The net radiative flux (or net radiation heat transfer rate, \(\left.q_{\mathrm{rad}}=q_{\mathrm{rad}}^{\prime \prime} A\right),\) is important because it affects temperature distribution. The quantities \(E, G,\) and \(J\) are used to compute \(q_{\mathrm{rad}}^{\prime \prime}.\) They are also important in applications involving radiation detection and temperature measurement.

Table 1. Radiative fluxes (over all wavelengths and in all directions)
Flux \(\left(\mathrm{W} / \mathrm{m}^{2}\right)\)	Description	Comment
Emissive power, \(E\)	Rate at which radiation is emitted from a surface per unit area	\(E=\varepsilon \sigma T_{s}^{4}\)
Irradiation, \(G\)	Rate at which radiation is incident upon a surface per unit area	Irradiation can be reflected, absorbed, or transmitted
Radiosity, \(J\)	Rate at which radiation leaves a surface per unit area	For an opaque surface \(J=E+\rho G\)
Net radiative flux \(q_{\text {rad }}^{\prime \prime}=J-G\)	Net rate of radiation leaving a surface per unit area	For an opaque surface \(q_{\mathrm{rad}}^{\prime \prime \prime}=\varepsilon \sigma T_{s}^{4}-\alpha G\)

Table 2. Radiation at a surface. (left) Reflection, absorption, and transmission of irradiation for a semitransparent medium. (right) The radiosity for an opaque medium.

4. Next steps

Directional effects are considered by introducing the concept of radiation intensity
Spectral effects are treated by introducing the concept of blackbody radiation
The emissive power of a real surface is connected to the concept of blackbody through the definition of emissivity.
The concept of a diffuse, gray surface, which has the property that \(\alpha=\varepsilon.\)
The interaction between solar radiation and radiation emitted by the earth’s surface.